-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480773 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542740 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 506482 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 736173 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2183439 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por magellanicLMC » Qua Fev 05, 2014 20:38
por magellanicLMC » Qua Fev 05, 2014 20:38
determine pelo teste da integral se a série é convergente ou divergente
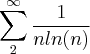
eu sei fazer o teste (é divergente) mas n consigo desenvolver as condições que seriam:
1) ser decrescente (provando pelo teste da derivada primeira
2) ter termos positivos p/
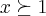
e ser contínua
mas n consigo calcular a derivada primeira (acredito que seja pela regra do quociente)
-
magellanicLMC
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 28, 2014 20:35
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qui Fev 06, 2014 11:55
por e8group » Qui Fev 06, 2014 11:55
Dica :
Defina
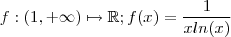
e considere
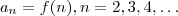
.
(i) Sempre
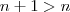
,então
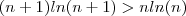
... ( qualquer função logarítmica é estritamente monótona)
(ii) Mostrar que
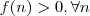
é o suficiente mostrar que
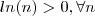
. Para tal , basta usar que

e que qualquer função logarítmica é estritamente monótona .Quanto a continuidade , se
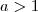
então o limite da função quando

é o próprio valor da função no ponto

(Fácil verificar) .
É isso . Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida de Série pelo teste da integral
por douglasnickson » Sáb Ago 20, 2016 13:41
- 0 Respostas
- 3741 Exibições
- Última mensagem por douglasnickson

Sáb Ago 20, 2016 13:41
Sequências
-
- [SÉRIE] Teste da comparação
por luiz1903 » Seg Fev 10, 2014 17:51
- 3 Respostas
- 2385 Exibições
- Última mensagem por e8group

Ter Fev 11, 2014 17:33
Sequências
-
- [SÉRIE] teste de comparação para convergência
por magellanicLMC » Ter Jan 28, 2014 20:47
- 5 Respostas
- 4844 Exibições
- Última mensagem por e8group

Sáb Fev 01, 2014 19:03
Sequências
-
- Teste da integral
por lucasguilherme2 » Qua Ago 29, 2012 23:23
- 2 Respostas
- 1431 Exibições
- Última mensagem por lucasguilherme2

Qui Ago 30, 2012 12:31
Sequências
-
- Série vira Integral
por Questioner » Dom Mai 23, 2010 13:12
- 3 Respostas
- 3654 Exibições
- Última mensagem por magellanicLMC

Qui Fev 06, 2014 23:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
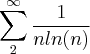
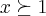 e ser contínua
e ser contínua 

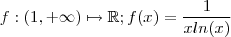 e considere
e considere 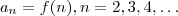 .
. 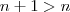 ,então
,então 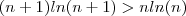 ... ( qualquer função logarítmica é estritamente monótona)
... ( qualquer função logarítmica é estritamente monótona) 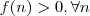 é o suficiente mostrar que
é o suficiente mostrar que 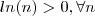 . Para tal , basta usar que
. Para tal , basta usar que  e que qualquer função logarítmica é estritamente monótona .Quanto a continuidade , se
e que qualquer função logarítmica é estritamente monótona .Quanto a continuidade , se 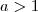 então o limite da função quando
então o limite da função quando  é o próprio valor da função no ponto
é o próprio valor da função no ponto  (Fácil verificar) .
(Fácil verificar) .
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.