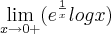 como calcular este limite?
como calcular este limite?

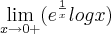 como calcular este limite?
como calcular este limite?
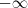 . Para ser mais preciso , basta mostra que para quaisquer seja um número real negativo dado é possível encontrar um número
. Para ser mais preciso , basta mostra que para quaisquer seja um número real negativo dado é possível encontrar um número 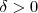 correspondente ,tal que se
correspondente ,tal que se 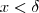 então
então 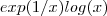 é estritamente menor que o número dado .Em símbolos ,
é estritamente menor que o número dado .Em símbolos , 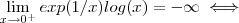 para todo
para todo  dado, existe
dado, existe 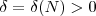 tal que se
tal que se 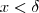 então
então 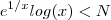 .
.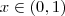 então
então 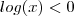 e
e 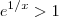 .Logo, multiplicando-se a segunda desigualdade por
.Logo, multiplicando-se a segunda desigualdade por 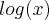 obtemos que
obtemos que 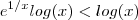 .
.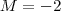 . Devemos encontrar um
. Devemos encontrar um  correspondente de
correspondente de 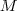 (notação
(notação 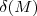 ) tal que se a desigualdade
) tal que se a desigualdade 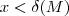 é verdadeira então obrigatoriamente
é verdadeira então obrigatoriamente 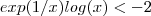 . Aplicando o log em
. Aplicando o log em 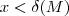 temos
temos 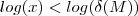 ,logo por transitividade
,logo por transitividade 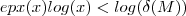 . Daí pondo
. Daí pondo 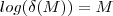 , resulta ,
, resulta , 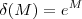 . Assim podemos concluir que dado
. Assim podemos concluir que dado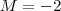 , tomando-se
, tomando-se 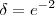 teremos que se
teremos que se 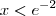 então
então 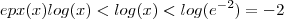 .
.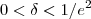 .
.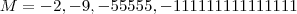 ou
ou 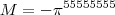 ... enfim qualquer que seja
... enfim qualquer que seja  basta por
basta por 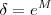 ou
ou 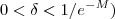 .Desta forma se
.Desta forma se 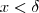 então
então 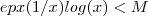 .
.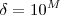 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

