[Limites] duas variáveis. Prova através da definição formal
Enviado: Sáb Jan 25, 2014 17:59Diga se o limite existe, se sim qual o valor.
![f(x,y)=\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/05bac8aad2413867e09f12b3ddfac115.png "f(x,y)=\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}")
o que eu fiz:
sabe-se que o ponto em questão é o (0.0).
fiz o limite através da reta x=0 e também da reta y=0. Em ambas o limite deu 2. Blz, mas não posso afirmar ainda que o limite é 2 !
Tentei usando a definição formal de limite, no caso de duas variáveis, isto é:
minha linha de raciocínio:
![\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1 \geq 0](/latexrender/pictures/bc6abacfc07d2e359363bf23ac223bbb.png "\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1 \geq 0")
![0 < \frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/872cd0851bac4eb69ee60cf82a566fd2.png "0 < \frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}")
Então:
![\left|\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right| < \left|\frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right|](/latexrender/pictures/fd959c7c454fc5c6af2203502b7e6e91.png "\left|\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right| < \left|\frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right|")
Mas vê-se também que pode-se tirar o módulo, ficando:
![\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2](/latexrender/pictures/a9a1c2020d3de2bf99d1984112e2fbbc.png "\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2")
Assim:
![\varepsilon = \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2](/latexrender/pictures/ff5711ea38c53430c506f2c5fe5a3d11.png "\varepsilon = \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2")
ficando...
![\delta = \sqrt[2]{(\varepsilon + 2 )\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/12244cabd76e673bb9e20b9a5f7a56f7.png "\delta = \sqrt[2]{(\varepsilon + 2 )\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}")
Assim, consegui encontrar uma relação entre épslon e delta. Sendo ambos positivos. Assim, existe limite e é igual a DOIS.
De fato a resposta do gabarito é dois. Porém não sei se minha prova está correta.
o que eu fiz:
sabe-se que o ponto em questão é o (0.0).
fiz o limite através da reta x=0 e também da reta y=0. Em ambas o limite deu 2. Blz, mas não posso afirmar ainda que o limite é 2 !
Tentei usando a definição formal de limite, no caso de duas variáveis, isto é:
minha linha de raciocínio:
Então:
Mas vê-se também que pode-se tirar o módulo, ficando:
Assim:
ficando...
Assim, consegui encontrar uma relação entre épslon e delta. Sendo ambos positivos. Assim, existe limite e é igual a DOIS.
De fato a resposta do gabarito é dois. Porém não sei se minha prova está correta.
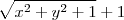.Desta forma ,temos 
(pois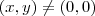 
) .Agora é simples computar o limite e até mesmo demonstra-ló pela definição .