 por marcosmuscul » Sáb Jan 25, 2014 17:59
por marcosmuscul » Sáb Jan 25, 2014 17:59
Diga se o limite existe, se sim qual o valor.
![f(x,y)=\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} f(x,y)=\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/05bac8aad2413867e09f12b3ddfac115.png)
o que eu fiz:
sabe-se que o ponto em questão é o (0.0).
fiz o limite através da reta x=0 e também da reta y=0. Em ambas o limite deu 2. Blz, mas não posso afirmar ainda que o limite é 2 !
Tentei usando a definição formal de limite, no caso de duas variáveis, isto é:

minha linha de raciocínio:
![\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1 \geq 0 \sqrt[2]{{x}^{2}+{y}^{2}+1}- 1 \geq 0](/latexrender/pictures/bc6abacfc07d2e359363bf23ac223bbb.png)
![0 < \frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} 0 < \frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/872cd0851bac4eb69ee60cf82a566fd2.png)
Então:
![\left|\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right| < \left|\frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right| \left|\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right| < \left|\frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right|](/latexrender/pictures/fd959c7c454fc5c6af2203502b7e6e91.png)
Mas vê-se também que pode-se tirar o módulo, ficando:
![\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2](/latexrender/pictures/a9a1c2020d3de2bf99d1984112e2fbbc.png)
Assim:
![\varepsilon = \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \varepsilon = \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2](/latexrender/pictures/ff5711ea38c53430c506f2c5fe5a3d11.png)
ficando...
![\delta = \sqrt[2]{(\varepsilon + 2 )\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} \delta = \sqrt[2]{(\varepsilon + 2 )\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/12244cabd76e673bb9e20b9a5f7a56f7.png)
Assim, consegui encontrar uma relação entre épslon e delta. Sendo ambos positivos. Assim, existe limite e é igual a DOIS.
De fato a resposta do gabarito é dois. Porém não sei se minha prova está correta.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por e8group » Seg Fev 03, 2014 20:10
por e8group » Seg Fev 03, 2014 20:10
Dica :
Multiplique ''em cima' e 'em baixo' por
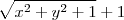
.Desta forma ,temos

(pois
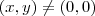
) .Agora é simples computar o limite e até mesmo demonstra-ló pela definição .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por marcosmuscul » Ter Fev 04, 2014 10:03
por marcosmuscul » Ter Fev 04, 2014 10:03
putz, um modo bem mais simples! rsrssr... valeu!
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites pela definição formal
por joaofonseca » Ter Out 11, 2011 09:38
- 1 Respostas
- 2755 Exibições
- Última mensagem por joaofonseca

Qua Out 12, 2011 19:29
Cálculo: Limites, Derivadas e Integrais
-
- [limites] Propriedades ou definição formal?
por jvabatista » Qua Jun 06, 2012 11:43
- 3 Respostas
- 3437 Exibições
- Última mensagem por adauto martins

Ter Out 14, 2014 20:05
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com a definição formal de limites
por Gustavooguto » Seg Out 13, 2014 23:49
- 1 Respostas
- 2372 Exibições
- Última mensagem por adauto martins

Ter Out 14, 2014 11:19
Funções
-
- Limites pela definição formal
por ramoncampos » Ter Nov 01, 2016 21:20
- 4 Respostas
- 9557 Exibições
- Última mensagem por ramoncampos

Sex Nov 04, 2016 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Limite através da definição
por Henrique Bueno » Sex Abr 19, 2013 00:25
- 1 Respostas
- 1426 Exibições
- Última mensagem por e8group

Sex Abr 19, 2013 02:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x,y)=\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} f(x,y)=\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/05bac8aad2413867e09f12b3ddfac115.png)

![\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1 \geq 0 \sqrt[2]{{x}^{2}+{y}^{2}+1}- 1 \geq 0](/latexrender/pictures/bc6abacfc07d2e359363bf23ac223bbb.png)
![0 < \frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} 0 < \frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/872cd0851bac4eb69ee60cf82a566fd2.png)
![\left|\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right| < \left|\frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right| \left|\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right| < \left|\frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \right|](/latexrender/pictures/fd959c7c454fc5c6af2203502b7e6e91.png)
![\frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \frac{{x}^{2}+{y}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 < \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2](/latexrender/pictures/a9a1c2020d3de2bf99d1984112e2fbbc.png)
![\varepsilon = \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2 \varepsilon = \frac{{\delta}^{2}}{\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} - 2](/latexrender/pictures/ff5711ea38c53430c506f2c5fe5a3d11.png)
![\delta = \sqrt[2]{(\varepsilon + 2 )\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1} \delta = \sqrt[2]{(\varepsilon + 2 )\sqrt[2]{{x}^{2}+{y}^{2}+1}- 1}](/latexrender/pictures/12244cabd76e673bb9e20b9a5f7a56f7.png)


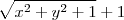 .Desta forma ,temos
.Desta forma ,temos  (pois
(pois 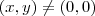 ) .Agora é simples computar o limite e até mesmo demonstra-ló pela definição .
) .Agora é simples computar o limite e até mesmo demonstra-ló pela definição .