 por jccp » Sex Jan 17, 2014 15:18
por jccp » Sex Jan 17, 2014 15:18
''Prove que a integral

é condicionalmente convergente.''
Tentei integrar de 0 a 1 e de 1 até infinito, mas começou a complicar e não entendi. Dá uma força aí, valeu.
-
jccp
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Out 06, 2013 14:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatua quimica
- Andamento: cursando
 por Man Utd » Sex Jan 17, 2014 20:26
por Man Utd » Sex Jan 17, 2014 20:26
jccp escreveu:''Prove que a integral

é condicionalmente convergente.''
Tentei integrar de 0 a 1 e de 1 até infinito, mas começou a complicar e não entendi. Dá uma força aí, valeu.
eu entendi o que quis fazer, eu tbm tentei utilizar o critério da comparação em vão.Esta integral encontra-se na matéria de integrais impróprias msm?
Minha resolução:
Sabemos da teoria de transformada de laplace :
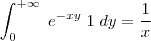
, então a nossa integral ficará:
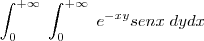
trocando a ordem de integração:
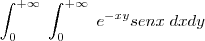
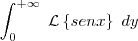
Lembrando que
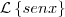
é uma notação para :
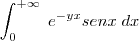
.
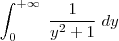
resolva para obter a resposta e concluir que é realmente convergente.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4622 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4590 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4348 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2848 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2873 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é condicionalmente convergente.''
é condicionalmente convergente.''
 é condicionalmente convergente.''
é condicionalmente convergente.''
é condicionalmente convergente.''
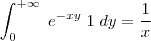 , então a nossa integral ficará:
, então a nossa integral ficará: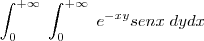
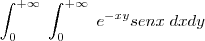
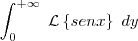
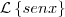 é uma notação para :
é uma notação para : 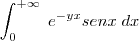 .
.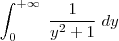


 .
.



