 por dimas_ant » Dom Dez 22, 2013 13:33
por dimas_ant » Dom Dez 22, 2013 13:33
Boa Tarde,
É minha primeira vez no forum e por isso pesso desculpa caso esteja cometendo algum erro.
Tenho uma prova de calculo na proxima quinta dia 26.
Tenho uma lista de exercícios para estudar, porém alguns não estou conseguindo resolver.
Pelo que li no forum posos postar apenas um exercicio por vez, segue um dos q estou com mais dificuldades:
4- Uma partícula move-se segundo a trajetória
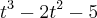
. O tempo está em segundos. Determine:
a) A velocidade no instante t=3s.
b) A aceleração no instante t= 1s.
Coloquei em anexo a lista completa, se alguem puder mi ajudar a resolve-la ficaria mt agradecido...
Estudar no natl é complicado, mas é minha ultima chance de passar na matéria
Desde já agradeço
Abraço
- Anexos
-

- Lista exercícios
-
dimas_ant
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Dez 22, 2013 13:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Lista de Exercícios - 1 / 2004
 por admin » Sáb Jul 21, 2007 05:36
por admin » Sáb Jul 21, 2007 05:36
- 0 Respostas
- 1411 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:36
Cálculo Numérico e Aplicações
-
- Gabarito Lista 1 de Exercícios - 2004
 por admin » Sáb Jul 21, 2007 05:51
por admin » Sáb Jul 21, 2007 05:51
- 0 Respostas
- 1463 Exibições
- Última mensagem por admin

Sáb Jul 21, 2007 05:51
Cálculo Numérico e Aplicações
-
- MAE1511 - lista de exercícios - 2003
 por admin » Ter Abr 22, 2008 22:35
por admin » Ter Abr 22, 2008 22:35
- 0 Respostas
- 1831 Exibições
- Última mensagem por admin

Ter Abr 22, 2008 22:35
Estatística para Licenciatura I
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 3299 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- Resolução dos Exercícios
por Carlinha » Qui Fev 26, 2009 17:03
- 1 Respostas
- 3691 Exibições
- Última mensagem por Molina

Sex Fev 27, 2009 21:01
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
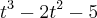 . O tempo está em segundos. Determine:
. O tempo está em segundos. Determine:
