(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Q. 20 - Pág.: 920)
Use a integral tripla para determinar o volume do sólido dado.
O sólido limitado pelos paraboloides y=x²+z² e y=8-x²-z²
Resolução:
Calcular o volume do sólido limitado pelos paraboloides dados, é o mesmo, em termos numéricos, que calcular o volume limitado pelos seguintes paraboloides: z=x²+y² e z=8-x²-y². O valor correspondente às unidades de volume é exatamente igual. Além disso, a forma como é apresentada as equações lembra as coordenadas cilíndricas, então será feito essa substituição. Antes, é importante determinar o conjunto ao qual será feita a integração. A ideia partirá de encontrar a interseção entre as superfícies:
Se z=z, então x²+y²=8-x²-y². Implica que 2x²+2y²=8, e portanto x²+y²=2². Esta última equação representa a circunferência de centro na origem e raio valendo 2 unidades.
Porém, em termos de domínio da função, tem-se que considerar o seguinte círculo:
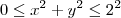
Mudança de Variável na Integral Tripla:
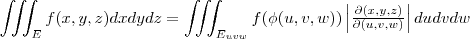
Onde:
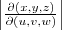 é o módulo do determinante jacobiano.
é o módulo do determinante jacobiano.Para o caso em específico feito por coordenadas cilíndricas:
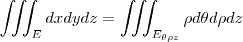
Imagine que o ângulo
 formado com o eixo das abscissas irá percorrer todos os ângulos para gerar o sólido que estamos calculando o volume, então
formado com o eixo das abscissas irá percorrer todos os ângulos para gerar o sólido que estamos calculando o volume, então 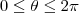 . Para o caso de
. Para o caso de 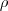 :
: 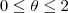 . A "componente z" irá de uma superfície a outra, ou seja, de
. A "componente z" irá de uma superfície a outra, ou seja, de 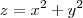 até
até 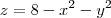 . Mas, em coordenadas cilíndricas:
. Mas, em coordenadas cilíndricas:  até
até 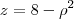 .
.Coordenadas Cilíndricas:
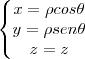
Integral Tripla:
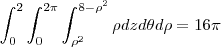 unidades de volume
unidades de volumePasso-a-passo:
a)
![\int_{\rho^2}^{8-\rho^2}\rho dz=\rho\int_{\rho^2}^{8-\rho^2} dz=\rho[(8-\rho^2)-(\rho^2)]=\rho(8-2\rho^2)=-2\rho^3+8\rho \int_{\rho^2}^{8-\rho^2}\rho dz=\rho\int_{\rho^2}^{8-\rho^2} dz=\rho[(8-\rho^2)-(\rho^2)]=\rho(8-2\rho^2)=-2\rho^3+8\rho](/latexrender/pictures/a6c9e902cc04caeb370e02310f2bad73.png)
b)
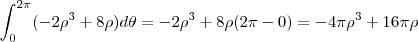
c)
![\int_0^2(-4\pi\rho^3+16\pi\rho)d\rho=4\pi[-\frac{\rho^4}{4}+2\rho^2]_0^2=16\pi \int_0^2(-4\pi\rho^3+16\pi\rho)d\rho=4\pi[-\frac{\rho^4}{4}+2\rho^2]_0^2=16\pi](/latexrender/pictures/2310a2a1372460ecb5b183985493ea1d.png)




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.