-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478004 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530454 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 494051 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 701905 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2114583 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Sobreira » Sáb Nov 30, 2013 15:00
por Sobreira » Sáb Nov 30, 2013 15:00
Olá amigos,
Estou tentando resolver este limite por L'Hospital mas nunca consigo eliminar a indeterminação...alguma idéia ???
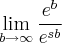
Se eu derivar seguidas vezes ainda não consigo eliminar a indeterminação

"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por e8group » Sáb Nov 30, 2013 15:27
por e8group » Sáb Nov 30, 2013 15:27
Lembre-se
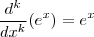
e que
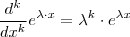
para qualquer natural

. Além disso note que
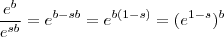
.Tem alguma informação sobre o número

? Se ele for menor que

segue que
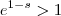
,caso contrário teremos
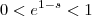
. Para concluir basta responder o que acontece com a função exponencial de base positiva e menor que 1 e com a de base maior que 1 lá no infinito .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sobreira » Sáb Nov 30, 2013 15:52
por Sobreira » Sáb Nov 30, 2013 15:52
Na realidade estou tentando encontrar a transformada de Laplace através da definição:
A função é f(t)=
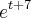
Como posso resolver ???
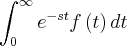
Depois de resolver a integral, quando considerei s>0 acabei caindo neste problema que ainda não consegui resolver. Se puder me ajudar, agradeço !!
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Sobreira » Sáb Nov 30, 2013 16:42
por Sobreira » Sáb Nov 30, 2013 16:42
Veja o que consegui até agora:
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por e8group » Sáb Nov 30, 2013 16:43
por e8group » Sáb Nov 30, 2013 16:43
Ainda não estudei Transformada de Laplace ,parece que isto é uma aplicação que leva uma função a outra (me corrija se eu estou errado ) . Posso tentar te ajudar com a integral imprópria . Sendo
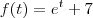
. Temos que
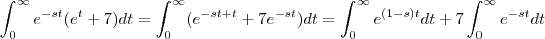
.
Agora faça as substituições simples
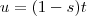
e
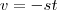
[/tex] as derivadas nos dá respectivamente ,
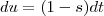
e
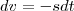
assuma a princípio que
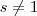
trataremos deste caso depois .Neste caso , teremos
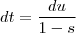
e
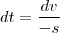
já que você considerou
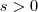
(ou seja ,
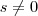
)
Vamos ter que considerar primeiro
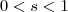
e segundo
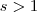
.
No primeiro caso temos que
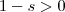
e
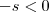
e assim quando
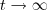
,
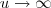
e
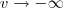
, quando

teremos também
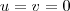
,renovando os limites de integração , a nova integral se escreve
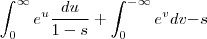
ou ainda
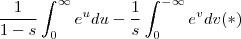
.
Calculando estas integrais obterá uma função da
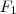
real a qual depende da variável

que pertence
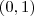
. (Isto se a integral convergir )
No segundo caso
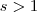
,então
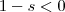
e
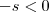
e assim , quando
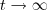
teremos que
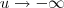
e
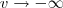
e como já vimos acima quando t =0 , v=u= 0 . Podemos usar a mesma expressão (*) apenas trocando os limites de integração e teremos outra função
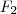
real dependendo da variável

a qual pertence
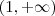
, dada por
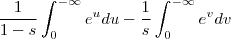
.
Portanto basta fazer estas contas são bem simples .
E finalmente se
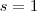
.
Teremos
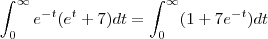
e esta integral não converge .
No final obterá uma função
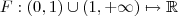
dada por
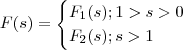
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sobreira » Sáb Nov 30, 2013 16:59
por Sobreira » Sáb Nov 30, 2013 16:59
Acho só que você viu errado a função:
A função é
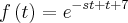
E não:
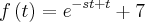
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por e8group » Sáb Nov 30, 2013 16:59
por e8group » Sáb Nov 30, 2013 16:59
Agora que vi
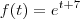
e não como eu tinha considerado . Neste caso é até mais fácil . Basta ver que
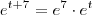
e portanto o integrando se escreve
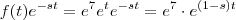
.
Basta desconsiderar aquela integral multiplicada por
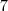
no post acima , e considerar a outra multiplicado por
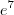
.
Assim terá de calcular :
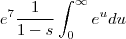
,
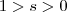
e
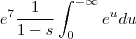
,
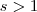
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sáb Nov 30, 2013 17:01
por e8group » Sáb Nov 30, 2013 17:01
Talvez ficou um pouco confuso . Se você não compreender só dizer .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Sobreira » Sáb Nov 30, 2013 17:21
por Sobreira » Sáb Nov 30, 2013 17:21
Então...
Eu realmente tenho ficado confuso naquela parte do asterisco...pq não eh somente neste exercício....já houve alguns outros que o problema ficava naquele termo do asterisco por não conseguir eliminar a indeterminação e vejo que a resposta está logo ali do outro lado esperando o resultado deste asterisco ser zero.
Até então os exercícios que eu fiz era considerado só duas condições: s>0 ou s<0.
Agora tentando entender melhor este exercício, mandei inclusive a foto, eu consegui sair deste problema utilizando aquelas condições acima e vi que só chegaria na resposta na condição de s>1. Como você disse você ainda não viu o conteúdo de Laplace, mas sua ideia está correta.
Agora pensando somente como uma integral imprópria, pelo que resolvi você considera correta minha preposição de que s tem que ser maior que 1 ???
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por e8group » Sáb Nov 30, 2013 17:37
por e8group » Sáb Nov 30, 2013 17:37
Sim concordo com você ,

será maior que 1 . Por quê a integral
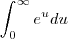
não converge (1>s>0) , já a outra
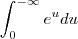
(s>1) converge . Você mesmo notou isto na sua solução pelo que vi . É isso .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como resolver limite exponencial
por joaofonseca » Sex Mar 30, 2012 12:59
- 2 Respostas
- 1940 Exibições
- Última mensagem por joaofonseca

Sáb Mar 31, 2012 11:15
Cálculo: Limites, Derivadas e Integrais
-
- limites como resolver sem L'hospital
 por eulercx » Qui Jan 14, 2016 10:37
por eulercx » Qui Jan 14, 2016 10:37
- 1 Respostas
- 3479 Exibições
- Última mensagem por RuuKaasu

Qui Jan 14, 2016 18:29
Cálculo: Limites, Derivadas e Integrais
-
- LIMITE COM L HOSPITAL
por geovane » Seg Out 03, 2016 18:17
- 1 Respostas
- 4789 Exibições
- Última mensagem por DanielFerreira

Sáb Nov 26, 2016 19:03
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] limite por L'Hospital
por beel » Seg Out 24, 2011 17:18
- 3 Respostas
- 1579 Exibições
- Última mensagem por LuizAquino

Ter Out 25, 2011 17:21
Cálculo: Limites, Derivadas e Integrais
-
- [CALCULO] limite - L'Hospital?
por beel » Dom Out 30, 2011 17:13
- 3 Respostas
- 1576 Exibições
- Última mensagem por LuizAquino

Dom Out 30, 2011 18:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 53 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
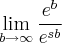


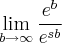


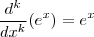 e que
e que 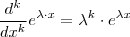 para qualquer natural
para qualquer natural  . Além disso note que
. Além disso note que 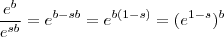 .Tem alguma informação sobre o número
.Tem alguma informação sobre o número  ? Se ele for menor que
? Se ele for menor que  segue que
segue que 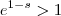 ,caso contrário teremos
,caso contrário teremos 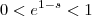 . Para concluir basta responder o que acontece com a função exponencial de base positiva e menor que 1 e com a de base maior que 1 lá no infinito .
. Para concluir basta responder o que acontece com a função exponencial de base positiva e menor que 1 e com a de base maior que 1 lá no infinito .
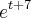
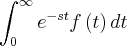


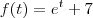 . Temos que
. Temos que 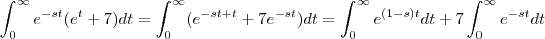 .
. 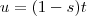 e
e 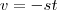 [/tex] as derivadas nos dá respectivamente ,
[/tex] as derivadas nos dá respectivamente , 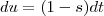 e
e 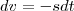 assuma a princípio que
assuma a princípio que 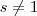 trataremos deste caso depois .Neste caso , teremos
trataremos deste caso depois .Neste caso , teremos 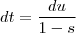 e
e 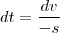 já que você considerou
já que você considerou 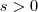 (ou seja ,
(ou seja ,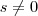 )
) 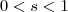 e segundo
e segundo 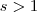 .
. 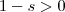 e
e 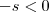 e assim quando
e assim quando 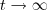 ,
,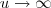 e
e 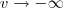 , quando
, quando  teremos também
teremos também 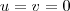 ,renovando os limites de integração , a nova integral se escreve
,renovando os limites de integração , a nova integral se escreve 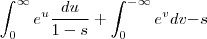 ou ainda
ou ainda 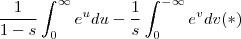 .
.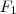 real a qual depende da variável
real a qual depende da variável  que pertence
que pertence 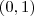 . (Isto se a integral convergir )
. (Isto se a integral convergir ) 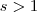 ,então
,então 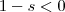 e
e 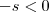 e assim , quando
e assim , quando 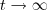 teremos que
teremos que 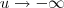 e
e 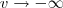 e como já vimos acima quando t =0 , v=u= 0 . Podemos usar a mesma expressão (*) apenas trocando os limites de integração e teremos outra função
e como já vimos acima quando t =0 , v=u= 0 . Podemos usar a mesma expressão (*) apenas trocando os limites de integração e teremos outra função 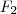 real dependendo da variável
real dependendo da variável  a qual pertence
a qual pertence 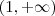 , dada por
, dada por 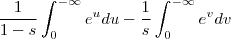 .
.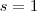 .
. 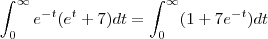 e esta integral não converge .
e esta integral não converge .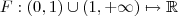 dada por
dada por 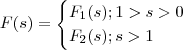 .
.
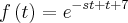
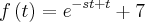

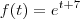 e não como eu tinha considerado . Neste caso é até mais fácil . Basta ver que
e não como eu tinha considerado . Neste caso é até mais fácil . Basta ver que 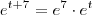 e portanto o integrando se escreve
e portanto o integrando se escreve 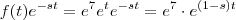 .
. 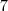 no post acima , e considerar a outra multiplicado por
no post acima , e considerar a outra multiplicado por 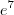 .
. 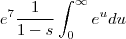 ,
, 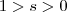 e
e 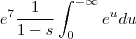 ,
, 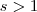 .
.


 será maior que 1 . Por quê a integral
será maior que 1 . Por quê a integral 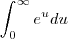 não converge (1>s>0) , já a outra
não converge (1>s>0) , já a outra 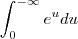 (s>1) converge . Você mesmo notou isto na sua solução pelo que vi . É isso .
(s>1) converge . Você mesmo notou isto na sua solução pelo que vi . É isso .
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?