-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 484498 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 546580 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 510387 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 741853 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2193977 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por raimundoocjr » Qui Out 17, 2013 21:55
por raimundoocjr » Qui Out 17, 2013 21:55
(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Q. 18 - Pág.: 810)
Determine o limite, se existir, ou mostre que não existe.

Resposta para o cálculo do limite: 0 (zero).
Coloquei a definição apenas para tentar clarear as ideias. Mas, se alguém conseguir responder por outro método, irá ajudar. Por exemplo, Teorema do Confronto, mudança de variável etc.
Definição de Limite de uma Função de Duas Variáveis (pelo menos):

(Livro: Cálculo - Autor: James Stewart - Volume 2 - 7ª Edição - Pág.: 804)
Como faço para provar esse limite?
-
raimundoocjr
-
 por Man Utd » Ter Jun 17, 2014 13:05
por Man Utd » Ter Jun 17, 2014 13:05
Olá:D
Esse limite não existe, vamos usar a regra dos caminhos :

Pelo caminho :
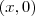
:

Agora por :

:


Assim como os valores são diferentes temos que o limite não existe.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite de duas variaveis
por Tixa11 » Seg Abr 01, 2013 13:13
- 1 Respostas
- 1880 Exibições
- Última mensagem por young_jedi

Qua Abr 03, 2013 11:09
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Duas variaveis
por fabriel » Sáb Jun 15, 2013 16:48
- 2 Respostas
- 2150 Exibições
- Última mensagem por temujin

Sáb Jun 15, 2013 19:10
Cálculo: Limites, Derivadas e Integrais
-
- Limite de Função de Duas Variáveis
por raimundoocjr » Qui Out 10, 2013 22:29
- 0 Respostas
- 1431 Exibições
- Última mensagem por raimundoocjr

Qui Out 10, 2013 22:29
Cálculo: Limites, Derivadas e Integrais
-
- [Limite Com Duas Variáveis] - Simplificação de Fração
por Vitor2+ » Dom Jul 08, 2012 03:19
- 2 Respostas
- 3998 Exibições
- Última mensagem por Vitor2+

Dom Jul 08, 2012 11:48
Cálculo: Limites, Derivadas e Integrais
-
- [Limite de Funções de duas variáveis] Demostração
por ARCS » Dom Out 21, 2012 20:15
- 1 Respostas
- 1953 Exibições
- Última mensagem por MarceloFantini

Dom Out 21, 2012 22:04
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




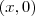 :
:
 :
:







