 por mateusprs22 » Dom Out 13, 2013 13:48
por mateusprs22 » Dom Out 13, 2013 13:48
Não consegui desenvolver a resolução, pq não ei como aplicar o TVI neste caso.
Mostre que x^3 + x^2 - 5x +1 =0 admite tres raizes reais e tente localizá-las
Por favor me ajudem!!!
-
mateusprs22
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Out 13, 2013 13:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Exatas
- Andamento: cursando
 por Bravim » Dom Out 13, 2013 20:11
por Bravim » Dom Out 13, 2013 20:11
Esse problema é mais de cálculo numérico que de cálculo I, mas aí vai.
Como f(x) é um polinômio está mais do que cara que ele é contínuo para todos os reais.
Bem, agora o que você deve fazer é derivar f(x).
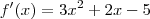
Com isso você encontra os pontos onde f(x) cresce ou decresce e fica mais fácil de você saber onde procurar os valores para o tvi.
Deste modo verificamos que
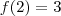
,
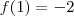
,

,
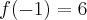
,
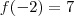
,
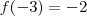
,
Neste casos nós teremos raízes desse polinômio entre [2,1], [1,0],[-3,-2].
Não sei se ficou muito claro para você como eu fiz, mas pense que como a função é contínua, se eu tenho um valor positivo para f(a) e um valor negativo para f(b) , a reta tem de passar por f(x)=0, não tem como ela dar saltos. Este teorema não é perfeito visto que ele me diz que entre [0,2] não tem raíz apesar de eu já ter dito que tem duas raízes neste intervalo, portanto também temos de verificar as derivadas para termos certeza se estamos fazendo direito. Para isso temos que verificar que a função é estritamente crescente ou decrescente neste intervalo, ou seja, verificar se a derivada muda de sinal ou não e claro a derivada tem de ser diferente de zero.

-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por mateusprs22 » Dom Out 13, 2013 20:37
por mateusprs22 » Dom Out 13, 2013 20:37
Valeu cara, Muuiito obrigado
-
mateusprs22
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Out 13, 2013 13:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias Exatas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6200 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4387 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2535 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 4926 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



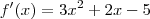
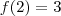 ,
, 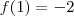 ,
,  ,
, 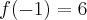 ,
,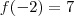 ,
,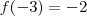 ,
, 




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.