![\int_{0}^{x}\sqrt[2]{(1 + {t}^{2})}dt](/latexrender/pictures/42dbc60910ef92a9245525e13cb09331.png "\int_{0}^{x}\sqrt[2]{(1 + {t}^{2})}dt")
Olá, estou com muita dificuldade para resolver esta integral, pois usando o método de substituição com u = t², dt =
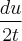e fica com duas variáveis diferentes , e usando u =![\sqrt[2]{(1 + {t}^{2})}](/latexrender/pictures/9e9614edd77cf27194752ad1a88e9f93.png "\sqrt[2]{(1 + {t}^{2})}")
, dt = ![\frac{t}{\sqrt[2]{(1 + {t}^{2})}}](/latexrender/pictures/2e47089e7237ab7757f74516a66c53a6.png "\frac{t}{\sqrt[2]{(1 + {t}^{2})}}")
fica mais complexo ainda, alguém pode me ajudar por favor.Obrigado
por Paulo Perez » Qui Out 03, 2013 12:22
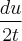e fica com duas variáveis diferentes , e usando u =, dt = fica mais complexo ainda, alguém pode me ajudar por favor.
por Bravim » Qui Out 03, 2013 16:45
![\sqrt[]{1+t^2}](/latexrender/pictures/b0568fda29fd8b09365f6b041041eaf4.png "\sqrt[]{1+t^2}")
, é melhor substituir por ![\sqrt[]{1+t^2}=sec(u)](/latexrender/pictures/f3c06e6be361815fad4c77c18b542671.png "\sqrt[]{1+t^2}=sec(u)")
por Paulo Perez » Sex Out 04, 2013 16:32
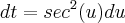
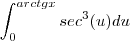
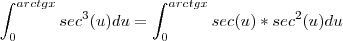
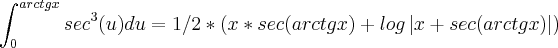
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)