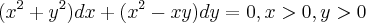
Fazendo o teste, vemos que os coeficientes da equação são funções homogêneas de mesmo grau. Então, fazendo y = vx, temos y' = v + xv' e substituindo na equação, obtemos:
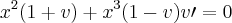 .
.Não entendi essa substituição, quando substituí não consegui chegar a esse resultado. Alguém pode me ajudar?
Outra dúvida é : tenho a seguinte equação linear diferencial não homogênea de primeira ordem
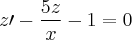
E a solução geral desta equação é dada por
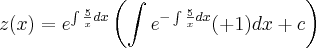
Não entendi consegui resolver esta equação. Tentei por método das separáveis, mas como é linear não homogênea, tenho que resolver assim, mas não consegui. Alguém consegue me explicar?
Obrigada!

