 por Pessoa Estranha » Dom Ago 25, 2013 12:40
por Pessoa Estranha » Dom Ago 25, 2013 12:40
Olá.... Estou com dificuldade para resolver a seguinte questão.
Seja
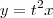
, onde
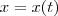
é uma função derivável. Calcule
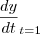
, supondo
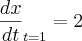
e x=3 para t=1.
Tentei resolver de duas maneiras.
Primeiro usei a regra do produto:
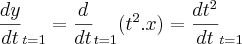
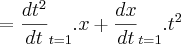
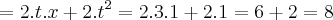
.
Esta é a resposta correta, porém eu também tentei resolver utilizando a regra da cadeia, mas deu errado.
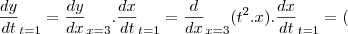
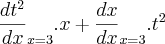
)
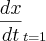
=6
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Dom Ago 25, 2013 14:04
por Pessoa Estranha » Dom Ago 25, 2013 14:04
Na verdade, na regra da cadeia, nas minhas contas, deu 2 e não 6.
-(a resposta certa é 8).
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Dom Ago 25, 2013 14:06
por Pessoa Estranha » Dom Ago 25, 2013 14:06
Pessoal, por favor, ajudem-me!!!! A prova é amanhã!!!!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Ago 25, 2013 16:31
por e8group » Dom Ago 25, 2013 16:31
Boa tarde . Sua primeira solução está correta . Observe que

é função real de uma variável real assim como a função
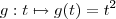
também o é .Como ambas funções possuem regras de associações dependentes da mesma variável

.Logo o produto destas funções fornecerá uma nova função cuja regra de associação(também só dependendo de

) desta função será
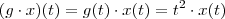
. Na minha opinião o resultado que temos que usar para derivar esta função é a regra do produto e não a regra da cadeia . Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Dom Ago 25, 2013 18:53
por Russman » Dom Ago 25, 2013 18:53
Aplique a regra do produto!
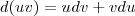
Assim,
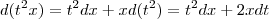
e
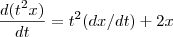
. Desse modo, para

, temos
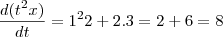
.
Regra da cadeia serve para FUNÇÕES COMPOSTAS, e não para o seu produto.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Pessoa Estranha » Dom Ago 25, 2013 19:38
por Pessoa Estranha » Dom Ago 25, 2013 19:38
Olá pessoal! Obrigada por terem respondido.
Estou estudando através de um livro de cálculo, e, nele, realmente está escrito que devemos aplicar a regra da cadeia em derivadas de funções compostas, porém, há uma parte que diz o seguinte:
"Sendo
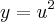
com
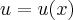
derivável, resulta
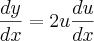
. Por outro lado,
![y={u}^{2}\Rightarrow \frac{dy}{du}=\frac{d}{du}[{u}^{2}]=2u y={u}^{2}\Rightarrow \frac{dy}{du}=\frac{d}{du}[{u}^{2}]=2u](/latexrender/pictures/f54952981d1a69e57a393a27c0954b0f.png)
. Assim,
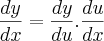
onde
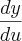
deve ser calculado em
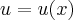
. Provaremos mais adiante que esta regra, conhecida como regra da cadeia, é válida sempre que
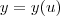
e
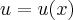
forem deriváveis".
Na última frase, realmente está claro que trata-se de funções compostas, mas no início eu entendi que a regra da cadeia poderia ser usada em casos como:
"Seja

com
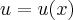
função derivável. Verifique que
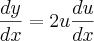
".
Este é, na verdade, bastante semelhante com o exercício que enviei aqui. Então pensei que pudesse ser assim, mas pelo visto fiz uma interpretação errada. O livro só confundiu-me!
Valeu pessoal! Obrigada pela ajuda!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 10508 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10716 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 12980 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14590 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 4973 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
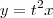 , onde
, onde 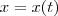 é uma função derivável. Calcule
é uma função derivável. Calcule 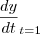 , supondo
, supondo 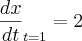 e x=3 para t=1.
e x=3 para t=1.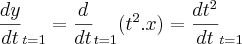
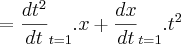
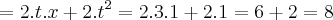 .
.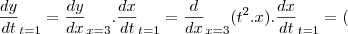
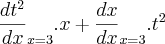 )
)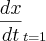 =6
=6


 é função real de uma variável real assim como a função
é função real de uma variável real assim como a função 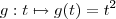 também o é .Como ambas funções possuem regras de associações dependentes da mesma variável
também o é .Como ambas funções possuem regras de associações dependentes da mesma variável  .Logo o produto destas funções fornecerá uma nova função cuja regra de associação(também só dependendo de
.Logo o produto destas funções fornecerá uma nova função cuja regra de associação(também só dependendo de 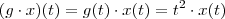 . Na minha opinião o resultado que temos que usar para derivar esta função é a regra do produto e não a regra da cadeia . Espero que ajude .
. Na minha opinião o resultado que temos que usar para derivar esta função é a regra do produto e não a regra da cadeia . Espero que ajude .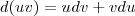
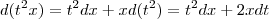 e
e 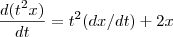 . Desse modo, para
. Desse modo, para  , temos
, temos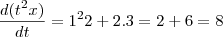 .
. com
com 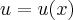 derivável, resulta
derivável, resulta 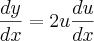 . Por outro lado,
. Por outro lado, ![y={u}^{2}\Rightarrow \frac{dy}{du}=\frac{d}{du}[{u}^{2}]=2u y={u}^{2}\Rightarrow \frac{dy}{du}=\frac{d}{du}[{u}^{2}]=2u](/latexrender/pictures/f54952981d1a69e57a393a27c0954b0f.png) . Assim,
. Assim, 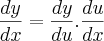 onde
onde 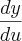 deve ser calculado em
deve ser calculado em 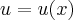 . Provaremos mais adiante que esta regra, conhecida como regra da cadeia, é válida sempre que
. Provaremos mais adiante que esta regra, conhecida como regra da cadeia, é válida sempre que 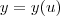 e
e 




