encontre a derivada de :
![f(x)= {\left[tg(x) \right]}^{{e}^{x}+4} f(x)= {\left[tg(x) \right]}^{{e}^{x}+4}](/latexrender/pictures/5b3a5910517da99b8b8e487852c1a26a.png)

![f(x)= {\left[tg(x) \right]}^{{e}^{x}+4} f(x)= {\left[tg(x) \right]}^{{e}^{x}+4}](/latexrender/pictures/5b3a5910517da99b8b8e487852c1a26a.png)

lucasdemirand escreveu:olá amigos, estou com uma duvida para a realização do seguinte problema,
encontre a derivada de :

 , onde
, onde  e
e  .
.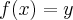 (apenas para facilitar), vem que:
(apenas para facilitar), vem que: .
.



![f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}+4).ln(tg(x))]´ f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}+4).ln(tg(x))]´](/latexrender/pictures/2ca4a017cae58d3efc36824e894b899b.png)
![(({e}^{x}+4).ln(tg(x))´= [({e}^{x}+4)´.ln(tg(x))]+[ln(tg(x)).({e}^{x}+4)]= (({e}^{x}+4).ln(tg(x))´= [({e}^{x}+4)´.ln(tg(x))]+[ln(tg(x)).({e}^{x}+4)]=](/latexrender/pictures/8d8f1b8c99d6015324f1b9d9ee5f0938.png)
![=[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)] =[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)]](/latexrender/pictures/390a4c444ede1456b17404d3bba85acd.png)
![f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)] f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)]](/latexrender/pictures/d0a4d51ee68e79dfb9c0535340683493.png)
 e a exponencial também de base
e a exponencial também de base  , pois uma é o inverso da outra. Depois, concluindo, apliquei o restante da fórmula de derivada de função composta. Pode ser que, às vezes, eu acabe errando em alguma conta, mas a ideia é esta.
, pois uma é o inverso da outra. Depois, concluindo, apliquei o restante da fórmula de derivada de função composta. Pode ser que, às vezes, eu acabe errando em alguma conta, mas a ideia é esta.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)