-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480776 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542746 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 506494 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 736204 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2183485 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por nakagumahissao » Qui Ago 15, 2013 11:04
por nakagumahissao » Qui Ago 15, 2013 11:04
Pessoal, não consegui resolver esta questão. Apenas consegui o esboço do gráfico que se trata de uma esfera e de um cone. O cone limita a parte inferior e parte da esfera, o limite superior.
Poderiam me ajudar por favor? A questão é a seguinte:
Calcule a integral:
![{I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV {I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV](/latexrender/pictures/db5b81b4fc0f561bab447ff493098c67.png)
Onde R é a região limitada por:
![z = \sqrt[]{2 - {x}^{2} - {y}^{2}} z = \sqrt[]{2 - {x}^{2} - {y}^{2}}](/latexrender/pictures/e1128b31491a40f553d7021da41db36f.png)
e
![z = \sqrt[]{{x}^{2} + {y}^{2}} z = \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/593fda6c93daf33d4379ead6624bbe20.png)
Tentei utilizar coordenadas esféricas, mas obtive uma coisa muito complicada de se resolver. Alguém saberia resolver esta questão?
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por young_jedi » Sex Ago 16, 2013 15:51
por young_jedi » Sex Ago 16, 2013 15:51
minha sugestão é uma mudança para coordenadas polares
ai teríamos que
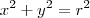
e
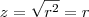
então a integral ficaria
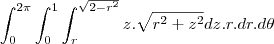
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por nakagumahissao » Sex Ago 16, 2013 16:35
por nakagumahissao » Sex Ago 16, 2013 16:35
Young_Jedi,
Vou tentar com polares, apesar de que o exercício foi dado para utilizarmos as coordenadas esféricas ou cilíndricas. Qualquer dúvida volto aqui novamente. Por enquanto, muitíssimo obrigado pela sua resposta.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por mecfael » Dom Ago 18, 2013 00:43
por mecfael » Dom Ago 18, 2013 00:43
Vamos usar coordenadas Cilíndricas para montar a integral, como temos uma região compreendida entre dois sólidos:
Onde o sólido de baixo

(cone)
E o sólido de cima é
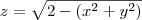
(esfera na origem de raio r²=2)
E a intersecção é igual a:
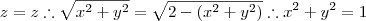
Uma circunferencia de raio r=1 no plano z=1, ou seja, as região será dividida da origem entre a parte do cone
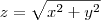
até z=1, e de z=1 até
a esfera
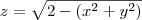
Então as regiões em coordenadas cilindricas
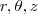
e
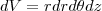
e
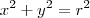
temos:
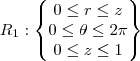
e
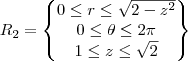
Os limites de R1 são os mesmos do cone, então é inútil explicar como achei, os limites de R2 temos que
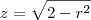
então se isolar o r temos que
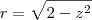
e verificamos que é verdade, pois em z=1, temos que o r=1 pois estamos na fronteira entre os dois sólidos que é a circunferência de raio r=1, e
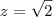
temos que r=0, pois é o máximo da região R2, agora que achamos R1 e R2 vamos montar a integral I dividida entre duas regiões:
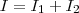
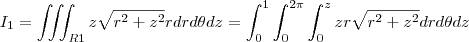
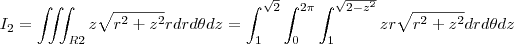
Essas integrais se resolvem com substituição simples fazendo
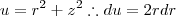
e de forma análoga para a variável z.
-
mecfael
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Ago 17, 2013 23:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrais Triplas
por wyncler » Sex Jul 03, 2009 23:04
- 0 Respostas
- 8402 Exibições
- Última mensagem por wyncler

Sex Jul 03, 2009 23:04
Cálculo: Limites, Derivadas e Integrais
-
- Integrais triplas
por ah001334 » Dom Dez 04, 2011 17:43
- 4 Respostas
- 3245 Exibições
- Última mensagem por ah001334

Dom Dez 04, 2011 19:05
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAIS TRIPLAS]
por carvalhothg » Sex Mai 04, 2012 11:23
- 1 Respostas
- 1858 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 00:29
Cálculo: Limites, Derivadas e Integrais
-
- Integrais Triplas
por gilijgs » Ter Nov 24, 2015 20:03
- 0 Respostas
- 2434 Exibições
- Última mensagem por gilijgs

Ter Nov 24, 2015 20:03
Cálculo: Limites, Derivadas e Integrais
-
- Mudança de variaveis em integrais duplas e triplas
por luiz3d » Qui Out 08, 2009 17:09
- 0 Respostas
- 3642 Exibições
- Última mensagem por luiz3d

Qui Out 08, 2009 17:09
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV {I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV](/latexrender/pictures/db5b81b4fc0f561bab447ff493098c67.png)
![z = \sqrt[]{2 - {x}^{2} - {y}^{2}} z = \sqrt[]{2 - {x}^{2} - {y}^{2}}](/latexrender/pictures/e1128b31491a40f553d7021da41db36f.png)
![z = \sqrt[]{{x}^{2} + {y}^{2}} z = \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/593fda6c93daf33d4379ead6624bbe20.png)

![{I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV {I}_{4} = \int_{R}^{}\int_{}^{}\int_{}^{}z\sqrt[]{{x}^{2} + {y}^{2} + {z}^{2}} dV](/latexrender/pictures/db5b81b4fc0f561bab447ff493098c67.png)
![z = \sqrt[]{2 - {x}^{2} - {y}^{2}} z = \sqrt[]{2 - {x}^{2} - {y}^{2}}](/latexrender/pictures/e1128b31491a40f553d7021da41db36f.png)
![z = \sqrt[]{{x}^{2} + {y}^{2}} z = \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/593fda6c93daf33d4379ead6624bbe20.png)

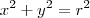
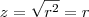
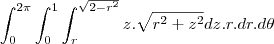


 (cone)
(cone)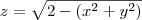 (esfera na origem de raio r²=2)
(esfera na origem de raio r²=2)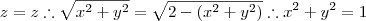
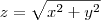 até z=1, e de z=1 até
até z=1, e de z=1 até 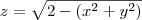
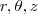 e
e 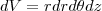 e
e 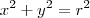
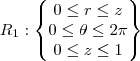
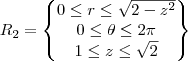
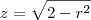 então se isolar o r temos que
então se isolar o r temos que 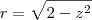 e verificamos que é verdade, pois em z=1, temos que o r=1 pois estamos na fronteira entre os dois sólidos que é a circunferência de raio r=1, e
e verificamos que é verdade, pois em z=1, temos que o r=1 pois estamos na fronteira entre os dois sólidos que é a circunferência de raio r=1, e 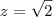 temos que r=0, pois é o máximo da região R2, agora que achamos R1 e R2 vamos montar a integral I dividida entre duas regiões:
temos que r=0, pois é o máximo da região R2, agora que achamos R1 e R2 vamos montar a integral I dividida entre duas regiões: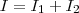
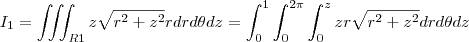
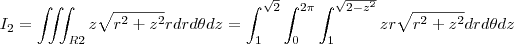
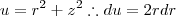 e de forma análoga para a variável z.
e de forma análoga para a variável z.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.