 por krtc » Qua Jul 24, 2013 02:07
por krtc » Qua Jul 24, 2013 02:07
Estou com dúvidas neste exercício:
Seja R a região limitada pela parábola

, pela reta y = 2x – 1 e pelo eixo x. Encontre o valor da área R.
Não sei se é pra calcular apenas a área acima do eixo x ou abaixo...pois a reta passa por -1 no eixo y e é tangente a parábola no ponto (1,1)...
Desde já, agradeço quem ajudar.
-
krtc
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 24, 2013 01:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Russman » Qua Jul 24, 2013 02:19
por Russman » Qua Jul 24, 2013 02:19
Ele quer que você calcule a areazinha em forma "quase" triangular, alí.
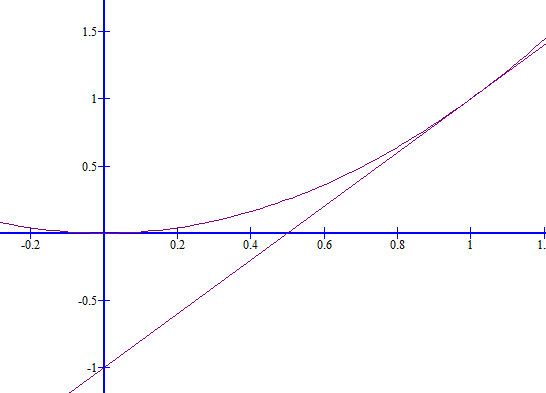
- graph
- graph (2).gif (3.96 KiB) Exibido 3717 vezes
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por krtc » Qua Jul 24, 2013 02:34
por krtc » Qua Jul 24, 2013 02:34
Russman escreveu:Ele quer que você calcule a areazinha em forma "quase" triangular, alí.
graph (2).gif
Ele quer que você calcule a areazinha em forma "quase" triangular, alí.
graph (2).gif
[/quote]
Então eu preciso calcular em função do y?
fazer
![x=\sqrt[]{y} x=\sqrt[]{y}](/latexrender/pictures/371065f56f4fad1c22d082bb674a29e1.png)
e
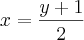
, ficando
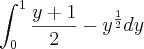
...tá certo o q eu fiz ou fiz besteira?
o resultado deu "
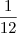
"
-
krtc
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 24, 2013 01:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Russman » Qua Jul 24, 2013 02:48
por Russman » Qua Jul 24, 2013 02:48
Pode fazer assim como tu fez, pq se deu
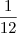
deve estar certo.
Eu faria a integral

"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por krtc » Qua Jul 24, 2013 02:54
por krtc » Qua Jul 24, 2013 02:54
Russman escreveu:Pode fazer assim como tu fez, pq se deu
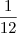
deve estar certo.
Eu faria a integral

Entendi! Eu pegava o intervalo errado para a reta!
Muito obrigado Russman!
-
krtc
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 24, 2013 01:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Russman » Qua Jul 24, 2013 03:13
por Russman » Qua Jul 24, 2013 03:13
Não, na integral em y o intervalo é de 0 à 1. Você fez certo. Só errou o sinal na integral que você postou.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4419 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- Área - Na próxima figura ABCD é um quadrilátero de área 200
 por marguiene » Sex Out 10, 2014 10:22
por marguiene » Sex Out 10, 2014 10:22
- 0 Respostas
- 2132 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:22
Geometria Plana
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2903 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2998 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Area
por karenblond » Qui Mar 25, 2010 17:19
- 6 Respostas
- 4173 Exibições
- Última mensagem por Molina

Ter Mar 30, 2010 00:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , pela reta y = 2x – 1 e pelo eixo x. Encontre o valor da área R.
, pela reta y = 2x – 1 e pelo eixo x. Encontre o valor da área R.


![x=\sqrt[]{y} x=\sqrt[]{y}](/latexrender/pictures/371065f56f4fad1c22d082bb674a29e1.png) e
e 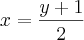 , ficando
, ficando 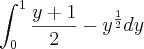 ...tá certo o q eu fiz ou fiz besteira?
...tá certo o q eu fiz ou fiz besteira?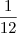 "
"