 por armando » Sáb Jul 20, 2013 15:22
por armando » Sáb Jul 20, 2013 15:22
Olá a todos.
Dada a função :
![f(x)=\sqrt[3]{\frac{3}{x^2}} f(x)=\sqrt[3]{\frac{3}{x^2}}](/latexrender/pictures/3aba0e9abab4f0ba5ddc428e9fa88019.png)
Tenho dúvidas quanto à solução dada no livro de onde retirei a questão. Que é como se segue:
![f^,(x)=-\frac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5} f^,(x)=-\frac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}](/latexrender/pictures/10452201c2b2f1c7eada127ab33aa66d.png)
Tanto quanto sei a fórmula para a derivada de uma raiz é :

ou, esta outra:
![y^,=\frac{1}{k\sqrt[k]{u^{k-1}}}\cdot u^, y^,=\frac{1}{k\sqrt[k]{u^{k-1}}}\cdot u^,](/latexrender/pictures/9dc847524b7f60ef3b880bb257f3e76b.png)
A derivada do radicando,
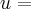

aplicando a fórmula de resolução do quociente dá
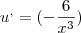
. Aplicando no lugar correto da/s fórmula/s, e desenvolvendo qualquer uma delas na integra deveríamos chegar á solução dada. Facto que aliás não consegui.
A minha dúvida é a seguinte:__ Será que a solução está errada ? Ou me estão faltando alguns artifícios matemáticos para conseguir chegar a ela ?
Gostava que alguém resolvesse a questão na integra,até à simplificação máxima para verificação, e assim tirar minha dúvida.
Grato pela atenção
armando
Editado pela última vez por
armando em Sáb Jul 20, 2013 16:17, em um total de 1 vez.
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusL » Sáb Jul 20, 2013 15:49
por MateusL » Sáb Jul 20, 2013 15:49
Armando, apesar de ter ficado meio vago o seu pedido, acredito, pelo título deste tópico, que queres descobrir a derivada de

Basta notar que:
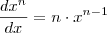
E que

pode ser escrito como:
![f(x)=\sqrt[3]{3}\cdot x^\frac{-2}{3} f(x)=\sqrt[3]{3}\cdot x^\frac{-2}{3}](/latexrender/pictures/77ede464f588caa699d9e91317e3f498.png)
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por armando » Sáb Jul 20, 2013 16:44
por armando » Sáb Jul 20, 2013 16:44
Olá MateusL .
É possível que o meu pedido lhe parecesse meio vago no momento em que você o viu. Dado que logo no início,quando o estava iniciando me descuidei, e sem querer clikei em Enviar. Creio que foi esse o motivo.
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusL » Sáb Jul 20, 2013 17:01
por MateusL » Sáb Jul 20, 2013 17:01
Armando, não seria
![f(x)=\sqrt[5]{\frac{3}{x^2}} f(x)=\sqrt[5]{\frac{3}{x^2}}](/latexrender/pictures/e288236abb7391f8f3db51c4d1a3f2d4.png)
?
Porque só assim o resultado iria fechar.
Se for, basta notar que:
![f(x)=\sqrt[5]{3}\cdot x^{-\frac{2}{5}} f(x)=\sqrt[5]{3}\cdot x^{-\frac{2}{5}}](/latexrender/pictures/7419eae39890ed57c091e8b620b854c9.png)
E, como
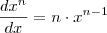
:
![\dfrac{df(x)}{dx}=\dfrac{d(\sqrt[5]{3}\cdot x^{-\frac{2}{5}})}{dx}=\sqrt[5]{3}\cdot \dfrac{d x^{-\frac{2}{5}}}{dx}=\sqrt[5]{3}\cdot \dfrac{-2}{5}\cdot x^{-\frac{2}{5}-1}=-\dfrac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}} \dfrac{df(x)}{dx}=\dfrac{d(\sqrt[5]{3}\cdot x^{-\frac{2}{5}})}{dx}=\sqrt[5]{3}\cdot \dfrac{d x^{-\frac{2}{5}}}{dx}=\sqrt[5]{3}\cdot \dfrac{-2}{5}\cdot x^{-\frac{2}{5}-1}=-\dfrac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}}](/latexrender/pictures/a409d25c37b6ad04d15e52b0b213b833.png)
Qualquer dúvida, só perguntar!
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por armando » Dom Jul 21, 2013 22:17
por armando » Dom Jul 21, 2013 22:17
Olá Mateus.
De facto você tinha razão. Na verdade eu me enganei ao transcrever o enunciado aqui para o fórum. Efetivamente, como pude verificar com mais atenção no livro de onde o saquei, em vez de raiz cubica, está de facto raiz quinta. Assim, já consegui chegar à solução por uma das fórmulas que referi.
Obrigado por compartilhar a sua perspicácia, e me alertar para o meu erro.
Abraço !
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite de função com raiz cúbica
por leandroassisc » Ter Mar 10, 2015 16:25
- 3 Respostas
- 3029 Exibições
- Última mensagem por leandroassisc

Ter Mar 10, 2015 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7459 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- log na base 1\5 de raiz cubica de 625 = 2x
por Nessa 2012 » Seg Nov 19, 2012 16:18
- 1 Respostas
- 3582 Exibições
- Última mensagem por Cleyson007

Seg Nov 19, 2012 16:31
Logaritmos
-
- Fatoração de raiz cúbica
por Paula Noia » Sáb Jun 15, 2013 21:22
- 2 Respostas
- 12290 Exibições
- Última mensagem por Paula Noia

Dom Jun 16, 2013 11:29
Cálculo: Limites, Derivadas e Integrais
-
- Limite raiz cúbica
por Carolminera » Qua Jul 16, 2014 18:25
- 0 Respostas
- 3554 Exibições
- Última mensagem por Carolminera

Qua Jul 16, 2014 18:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=\sqrt[3]{\frac{3}{x^2}} f(x)=\sqrt[3]{\frac{3}{x^2}}](/latexrender/pictures/3aba0e9abab4f0ba5ddc428e9fa88019.png)
![f^,(x)=-\frac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5} f^,(x)=-\frac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}](/latexrender/pictures/10452201c2b2f1c7eada127ab33aa66d.png)

![y^,=\frac{1}{k\sqrt[k]{u^{k-1}}}\cdot u^, y^,=\frac{1}{k\sqrt[k]{u^{k-1}}}\cdot u^,](/latexrender/pictures/9dc847524b7f60ef3b880bb257f3e76b.png)

 aplicando a fórmula de resolução do quociente dá
aplicando a fórmula de resolução do quociente dá 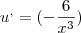 . Aplicando no lugar correto da/s fórmula/s, e desenvolvendo qualquer uma delas na integra deveríamos chegar á solução dada. Facto que aliás não consegui.
. Aplicando no lugar correto da/s fórmula/s, e desenvolvendo qualquer uma delas na integra deveríamos chegar á solução dada. Facto que aliás não consegui.


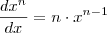
![f(x)=\sqrt[3]{3}\cdot x^\frac{-2}{3} f(x)=\sqrt[3]{3}\cdot x^\frac{-2}{3}](/latexrender/pictures/77ede464f588caa699d9e91317e3f498.png)

![f(x)=\sqrt[5]{\frac{3}{x^2}} f(x)=\sqrt[5]{\frac{3}{x^2}}](/latexrender/pictures/e288236abb7391f8f3db51c4d1a3f2d4.png) ?
?![f(x)=\sqrt[5]{3}\cdot x^{-\frac{2}{5}} f(x)=\sqrt[5]{3}\cdot x^{-\frac{2}{5}}](/latexrender/pictures/7419eae39890ed57c091e8b620b854c9.png)
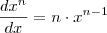 :
:![\dfrac{df(x)}{dx}=\dfrac{d(\sqrt[5]{3}\cdot x^{-\frac{2}{5}})}{dx}=\sqrt[5]{3}\cdot \dfrac{d x^{-\frac{2}{5}}}{dx}=\sqrt[5]{3}\cdot \dfrac{-2}{5}\cdot x^{-\frac{2}{5}-1}=-\dfrac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}} \dfrac{df(x)}{dx}=\dfrac{d(\sqrt[5]{3}\cdot x^{-\frac{2}{5}})}{dx}=\sqrt[5]{3}\cdot \dfrac{d x^{-\frac{2}{5}}}{dx}=\sqrt[5]{3}\cdot \dfrac{-2}{5}\cdot x^{-\frac{2}{5}-1}=-\dfrac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}}](/latexrender/pictures/a409d25c37b6ad04d15e52b0b213b833.png)
