 por ghiza » Seg Jul 15, 2013 11:27
por ghiza » Seg Jul 15, 2013 11:27
![\int \sqrt[]{t^2+2t^4} dt \int \sqrt[]{t^2+2t^4} dt](/latexrender/pictures/ce58fb30d62484c0e90280eb60c20f95.png)
se eu substituir
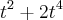
por u, chegarei ao resultado correto?
-
ghiza
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Jul 14, 2013 21:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng. alimentos
- Andamento: cursando
 por e8group » Seg Jul 15, 2013 12:19
por e8group » Seg Jul 15, 2013 12:19
Bom dia . Note que
![\sqrt{t^2 + 4t^4} = \sqrt{t^2[1+4t^2]} = \sqrt{t^2} \sqrt{1+4t^2} = |t|\sqrt{1+4t^2} \sqrt{t^2 + 4t^4} = \sqrt{t^2[1+4t^2]} = \sqrt{t^2} \sqrt{1+4t^2} = |t|\sqrt{1+4t^2}](/latexrender/pictures/0dc1a8122fb60d78a928e5376b534eb4.png)
.Assim , se
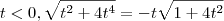
. Caso

.Vemos que em ambos casos a substituição simples
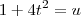
resolve o problema .
Tente concluir e comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] dúvida - integral definida com raiz
por beel » Sex Nov 18, 2011 14:28
- 1 Respostas
- 2427 Exibições
- Última mensagem por MarceloFantini

Sex Nov 18, 2011 16:25
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Cos ( Raiz (t) ) / Raiz (t)
por Elvis » Seg Ago 24, 2015 16:28
- 0 Respostas
- 1060 Exibições
- Última mensagem por Elvis

Seg Ago 24, 2015 16:28
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Cos ( Raiz (t) ) / Raiz (t)
por Elvis » Seg Ago 24, 2015 16:23
- 1 Respostas
- 3085 Exibições
- Última mensagem por adauto martins

Ter Ago 25, 2015 15:15
Cálculo: Limites, Derivadas e Integrais
-
- Integral com raiz quadrada
por lalmeida » Sex Mai 02, 2014 00:49
- 1 Respostas
- 4349 Exibições
- Última mensagem por alienante

Sáb Mai 03, 2014 15:32
Cálculo: Limites, Derivadas e Integrais
-
- integral envolvendo raiz quadrada
por ronnmmaia » Sex Set 23, 2011 19:50
- 2 Respostas
- 24350 Exibições
- Última mensagem por ronnmmaia

Sáb Set 24, 2011 11:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int \sqrt[]{t^2+2t^4} dt \int \sqrt[]{t^2+2t^4} dt](/latexrender/pictures/ce58fb30d62484c0e90280eb60c20f95.png)
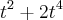 por u, chegarei ao resultado correto?
por u, chegarei ao resultado correto?
![\int \sqrt[]{t^2+2t^4} dt \int \sqrt[]{t^2+2t^4} dt](/latexrender/pictures/ce58fb30d62484c0e90280eb60c20f95.png)
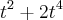 por u, chegarei ao resultado correto?
por u, chegarei ao resultado correto?
![\sqrt{t^2 + 4t^4} = \sqrt{t^2[1+4t^2]} = \sqrt{t^2} \sqrt{1+4t^2} = |t|\sqrt{1+4t^2} \sqrt{t^2 + 4t^4} = \sqrt{t^2[1+4t^2]} = \sqrt{t^2} \sqrt{1+4t^2} = |t|\sqrt{1+4t^2}](/latexrender/pictures/0dc1a8122fb60d78a928e5376b534eb4.png) .Assim , se
.Assim , se 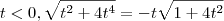 . Caso
. Caso  .Vemos que em ambos casos a substituição simples
.Vemos que em ambos casos a substituição simples 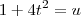 resolve o problema .
resolve o problema .
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.