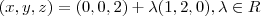
e
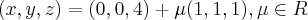
respectivamente. Determine
 e
e 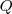 , com
, com 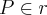 e
e 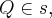 de modo que a distância de P e Q seja a menor possível.
de modo que a distância de P e Q seja a menor possível.Bem, essa questão esta na seção de máximos e mínimos do meu livro de cálculo de varias variaveis em que estudo. Embora tenha resposta abaixo, eu não consigo entender em como ele obteu a resposta, se alguem puder ajudar...
Resposta:
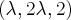 e
e 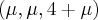 são pontos arbitrários de
são pontos arbitrários de  e
e  , respectivamente:
, respectivamente:![\sqrt[]{{(\lambda-\mu)}^{2}+{(2\lambda-\mu)}^{2}+{(2+\mu)}^{2}} \sqrt[]{{(\lambda-\mu)}^{2}+{(2\lambda-\mu)}^{2}+{(2+\mu)}^{2}}](/latexrender/pictures/75a00b818e697cba16ee371ed6f8931f.png) é a distância entre eles.
é a distância entre eles. Basta, então, determinar
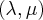 que minimiza
que minimiza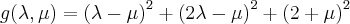 .
.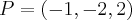 e
e 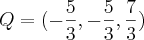



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)