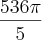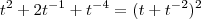por fabriel » Seg Mai 06, 2013 00:04
por fabriel » Seg Mai 06, 2013 00:04
Ola pessoal estou com uma duvida aqui na resolução deste exercicio:
Ache a área da superfice gerada pela revolução da curva em torno da eixo-y.
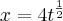
e
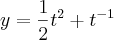
;
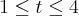
A área será
![\int_{1}^{4}2\pi x(t)\sqrt[]{{\left(\frac{dx}{st} \right)}^{2}+{\left(\frac{dy}{dt} \right)}^{2}}dt=2\pi\int_{1}^{4}4{t}^{\frac{1}{2}}\sqrt[]{{\left(2{t}^{-\frac{1}{2}} \right)}^{2}+{\left(t-{t}^{-2} \right)}^{2}}dt \int_{1}^{4}2\pi x(t)\sqrt[]{{\left(\frac{dx}{st} \right)}^{2}+{\left(\frac{dy}{dt} \right)}^{2}}dt=2\pi\int_{1}^{4}4{t}^{\frac{1}{2}}\sqrt[]{{\left(2{t}^{-\frac{1}{2}} \right)}^{2}+{\left(t-{t}^{-2} \right)}^{2}}dt](/latexrender/pictures/a456cbf47fbfffe2406bcb5034aa5772.png)
arrumando isso teremos:
![8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{{t}^{2}+2{t}^{-1}+{t}^{-4}}dt=8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{\left(t+{t}^{-2} \right)}dt 8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{{t}^{2}+2{t}^{-1}+{t}^{-4}}dt=8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{\left(t+{t}^{-2} \right)}dt](/latexrender/pictures/7932f2f9b01986247f7c887bc5f0ad83.png)
só que dai, não consigo sair resolver essa integral, o que eu tenho que fazer??
A resposta é
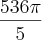
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por young_jedi » Ter Mai 07, 2013 23:54
por young_jedi » Ter Mai 07, 2013 23:54
veja que você pode dizer que
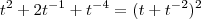
então você consegue tira isso da raiz e fazer a integração mais facilmente
comente qualquer coisa
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INTEGRAL DEFINIDA] Achar a área
por fabriel » Sex Dez 28, 2012 13:34
- 1 Respostas
- 2462 Exibições
- Última mensagem por MarceloFantini

Sex Dez 28, 2012 16:43
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida - ÁREA
por cardoed001 » Sáb Mar 22, 2014 19:04
- 2 Respostas
- 2316 Exibições
- Última mensagem por cardoed001

Dom Mar 23, 2014 12:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral, achar a área da região entre as curvas
por Janoca » Sex Jun 06, 2014 17:24
- 5 Respostas
- 4957 Exibições
- Última mensagem por alienante

Dom Jun 15, 2014 21:42
Cálculo: Limites, Derivadas e Integrais
-
- Duvida como achar a area do triangulo
 por renataf » Qui Dez 09, 2010 19:48
por renataf » Qui Dez 09, 2010 19:48
- 5 Respostas
- 4580 Exibições
- Última mensagem por Jefferson

Sáb Dez 11, 2010 22:45
Geometria Analítica
-
- Duvida para achar Area entre curvas
por gabrielnandi » Qua Mai 30, 2012 18:23
- 4 Respostas
- 3358 Exibições
- Última mensagem por gabrielnandi

Seg Jun 18, 2012 01:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
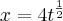 e
e 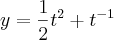 ;
; 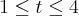
![\int_{1}^{4}2\pi x(t)\sqrt[]{{\left(\frac{dx}{st} \right)}^{2}+{\left(\frac{dy}{dt} \right)}^{2}}dt=2\pi\int_{1}^{4}4{t}^{\frac{1}{2}}\sqrt[]{{\left(2{t}^{-\frac{1}{2}} \right)}^{2}+{\left(t-{t}^{-2} \right)}^{2}}dt \int_{1}^{4}2\pi x(t)\sqrt[]{{\left(\frac{dx}{st} \right)}^{2}+{\left(\frac{dy}{dt} \right)}^{2}}dt=2\pi\int_{1}^{4}4{t}^{\frac{1}{2}}\sqrt[]{{\left(2{t}^{-\frac{1}{2}} \right)}^{2}+{\left(t-{t}^{-2} \right)}^{2}}dt](/latexrender/pictures/a456cbf47fbfffe2406bcb5034aa5772.png)
![8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{{t}^{2}+2{t}^{-1}+{t}^{-4}}dt=8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{\left(t+{t}^{-2} \right)}dt 8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{{t}^{2}+2{t}^{-1}+{t}^{-4}}dt=8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{\left(t+{t}^{-2} \right)}dt](/latexrender/pictures/7932f2f9b01986247f7c887bc5f0ad83.png)
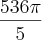

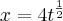 e
e 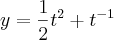 ;
; 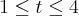
![\int_{1}^{4}2\pi x(t)\sqrt[]{{\left(\frac{dx}{st} \right)}^{2}+{\left(\frac{dy}{dt} \right)}^{2}}dt=2\pi\int_{1}^{4}4{t}^{\frac{1}{2}}\sqrt[]{{\left(2{t}^{-\frac{1}{2}} \right)}^{2}+{\left(t-{t}^{-2} \right)}^{2}}dt \int_{1}^{4}2\pi x(t)\sqrt[]{{\left(\frac{dx}{st} \right)}^{2}+{\left(\frac{dy}{dt} \right)}^{2}}dt=2\pi\int_{1}^{4}4{t}^{\frac{1}{2}}\sqrt[]{{\left(2{t}^{-\frac{1}{2}} \right)}^{2}+{\left(t-{t}^{-2} \right)}^{2}}dt](/latexrender/pictures/a456cbf47fbfffe2406bcb5034aa5772.png)
![8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{{t}^{2}+2{t}^{-1}+{t}^{-4}}dt=8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{\left(t+{t}^{-2} \right)}dt 8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{{t}^{2}+2{t}^{-1}+{t}^{-4}}dt=8\pi\int_{1}^{4}{t}^{\frac{1}{2}}\sqrt[]{\left(t+{t}^{-2} \right)}dt](/latexrender/pictures/7932f2f9b01986247f7c887bc5f0ad83.png)