 por marcosmuscul » Sáb Abr 13, 2013 14:07
por marcosmuscul » Sáb Abr 13, 2013 14:07
encontre o valor de a que satisfaça a igualdade.
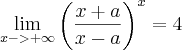
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por e8group » Sáb Abr 13, 2013 14:41
por e8group » Sáb Abr 13, 2013 14:41
Dicas :
(i) 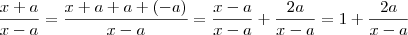
.
(ii) Faça a mudança de variável para
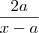
.Pergunta : Quando
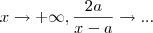
?
(iii) Veja o limite fundamental que resulta o
número de Euler OBS.: Acredito que seja não seja necessário usarmos a regra de L'hospital .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada]Regra da Cadeia, me ajudem nesse problema.
por marcosmuscul » Seg Abr 01, 2013 20:22
- 2 Respostas
- 1546 Exibições
- Última mensagem por e8group

Seg Abr 01, 2013 21:12
Cálculo: Limites, Derivadas e Integrais
-
- Me ajudem nesse exercicio!
por Catalao » Qui Nov 01, 2012 20:16
- 1 Respostas
- 1475 Exibições
- Última mensagem por MarceloFantini

Qui Nov 01, 2012 22:59
Geometria Analítica
-
- Me ajudem nesse exercício pfvr!
por andrebessas » Dom Jun 16, 2013 16:45
- 0 Respostas
- 3434 Exibições
- Última mensagem por andrebessas

Dom Jun 16, 2013 16:45
Funções
-
- Ajudem nesse exercício de análise combinatória?
por flor_de_lotus1 » Seg Jun 18, 2012 20:09
- 2 Respostas
- 2221 Exibições
- Última mensagem por fraol

Sáb Ago 11, 2012 15:47
Estatística
-
- [calculo] me ajudem nesse exercicio que eu não entendo
por amanda s » Sáb Nov 16, 2013 17:20
- 1 Respostas
- 1315 Exibições
- Última mensagem por Pessoa Estranha

Sáb Nov 16, 2013 21:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
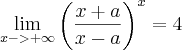


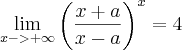

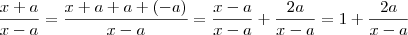 .
. 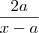 .Pergunta : Quando
.Pergunta : Quando 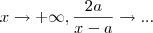 ?
? 

 .
.



