-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477668 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528309 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 491866 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 695729 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2103734 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Douglas16 » Dom Mar 31, 2013 16:36
por Douglas16 » Dom Mar 31, 2013 16:36
Determinar os valores das constantes

e

de tal forma que
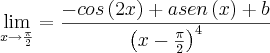
exista.
Depois, calcular o limite.
A única conclusão ou informação que consegui até agora é que b=-(a+1), isso vem do fato que para o valor limite existir, uma das condições é que tanto o limite do denominador quanto do numerador devem ser igual a zero, e a outra condição é a expressão seja tal que através do

eu possa eliminar a indeterminação

, ou seja eliminar
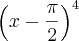
.
Mas não vejo uma forma de fazer isso.
Tentei fazer a substituição:
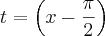
, mas ainda não vejo uma saída.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Douglas16 » Dom Mar 31, 2013 19:31
por Douglas16 » Dom Mar 31, 2013 19:31
A expressão do numerador pode ser fatorada como:

, admitindo x=-4.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 31, 2013 20:23
por e8group » Dom Mar 31, 2013 20:23
Considere :
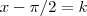
quando
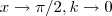
.
O limite a ser calculado será então :
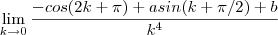
ou
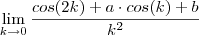
ou
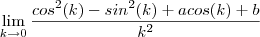
ou ainda ,
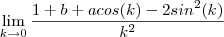
.
Mas,
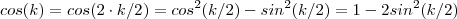
, então :
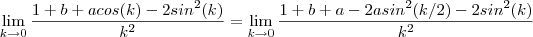
vemos então que o limite existe se ,e somente se ,

(Por quê ?)
Ou seja ,dado um

(ou

) real ,temos que
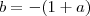
(ou
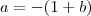
.) .Nestas condições o limite existirá .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Dom Mar 31, 2013 22:44
por Douglas16 » Dom Mar 31, 2013 22:44
Isso eu sei.
Mas considerando que a expressão do numerador pode ser fatorada como uma expressão quadrática em dois fatores:
Considerando X=
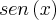
, tenho que: 2X²+aX-(a+2)=(2X+a+2)(X-1) (expressão 1)
Logo vejo que o fator que possui a constante a, só zera quando a=-4 e usando este valor para encontrar o de b=3, sei que esse são os valores constantes, mas não sei como e porquê.
Para mim, o valor de a na expressão 1, deve ser tal que contenha o fator k^4, para eliminar a indeterminação.
Depois fazer a resolução para encontrar o valor limite.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 31, 2013 23:41
por e8group » Dom Mar 31, 2013 23:41
Na minha opinião ,sua solução não faz sentido ,qual finalidade de adotar este método ? Além do mais ,no denominador temos um polinômio enquanto no numerador não,portanto, não faz sentido a seguinte frase :
Douglas16 escreveu:Para mim, o valor de a na expressão 1, deve ser tal que contenha o fator k^4, para eliminar a indeterminação.
Depois fazer a resolução para encontrar o valor limite.
É isso ,caso dúvidas retorne .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Seg Abr 01, 2013 02:16
por Douglas16 » Seg Abr 01, 2013 02:16
Quanto ao polinômio, o correto é que eu teria de dizer: Deve-se eliminar a indeterminação

, eliminando ou assimilando por alguma identidade o termo
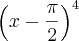
.
Agora veja se estou resolvendo corretamente:
Para que o limite exista:
(1)
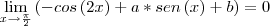
(equação 1)
Portanto

,
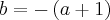
(equação 2)
(2) Deve-se eliminar a indeterminação

, eliminando ou assimilando por alguma identidade o termo
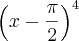
.
Fazendo a substituição da equação 2 na equação 1:

Fazendo X=
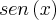
, tenho que:
2X²+

*X-

=(2X+a+2)(X-1) (equação 3)
Se X-1=
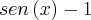
e
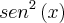
-1=
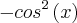
e
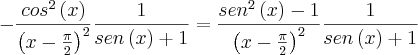
e de
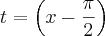
, portanto
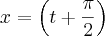
(equação 4),
Portanto:
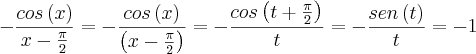
Assim (equação 3)/
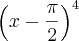
, fica: [(2X+a+2)/
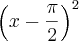
]*
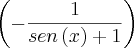
E para que o limite exista 2X+a+2=0 quando
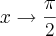
, portanto a=-4 e b=3.
Portanto o limite é
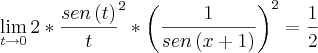
.
Concluindo:

e

. O valor do limite é

.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Seg Abr 01, 2013 13:31
por e8group » Seg Abr 01, 2013 13:31
Agora que observei que cometi um equívoco ,na verdade é
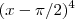
e não
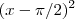
,fazendo
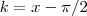
fica no denominador
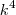
e não
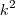
.Caso fosse
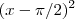
no denominador ,fixado
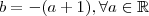
o limite sempre existiria, como mostra o wolframalpha :
http://www.wolframalpha.com/input/?i=li ... to++pi%2F2 , como não é o caso ,temos que impor mais condições sobre "a" e "b" .Peço desculpas pelo equívoco , parabéns pela dedicação a questão ,concluiu corretamente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quais os possíveis valores que satisfazem os valores reais
por andersontricordiano » Seg Fev 24, 2014 22:53
- 1 Respostas
- 4619 Exibições
- Última mensagem por Russman

Ter Fev 25, 2014 02:17
Números Complexos
-
- constantes de proporcionalidades
por Fabricio dalla » Qui Mar 31, 2011 17:47
- 1 Respostas
- 1386 Exibições
- Última mensagem por Elcioschin

Qui Mar 31, 2011 19:09
Álgebra Elementar
-
- QUESTÃO INTEGRAL COM CONSTANTES!
por iel » Seg Jun 01, 2009 22:38
- 1 Respostas
- 2936 Exibições
- Última mensagem por Molina

Ter Jun 02, 2009 06:24
Cálculo: Limites, Derivadas e Integrais
-
- (Limites) Encontrar as constantes
 por Haahs » Qua Nov 04, 2009 00:32
por Haahs » Qua Nov 04, 2009 00:32
- 7 Respostas
- 6097 Exibições
- Última mensagem por Lucio Carvalho

Dom Abr 20, 2014 20:32
Cálculo
-
- Limites com constantes positivas
por EulaCarrara » Qua Abr 21, 2010 15:59
- 2 Respostas
- 1902 Exibições
- Última mensagem por MarceloFantini

Qua Abr 21, 2010 18:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 22 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  de tal forma que
de tal forma que 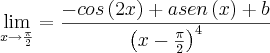 exista.
exista. eu possa eliminar a indeterminação
eu possa eliminar a indeterminação  , ou seja eliminar
, ou seja eliminar 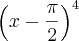 .
.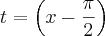 , mas ainda não vejo uma saída.
, mas ainda não vejo uma saída.

 , admitindo x=-4.
, admitindo x=-4.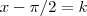 quando
quando 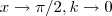 .
.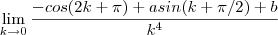 ou
ou 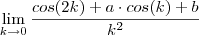 ou
ou 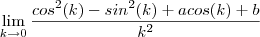 ou ainda ,
ou ainda , 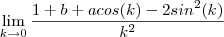 .
. 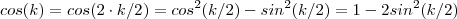 , então :
, então : 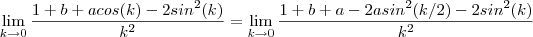
 (Por quê ?)
(Por quê ?)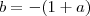 (ou
(ou 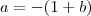 .) .Nestas condições o limite existirá .
.) .Nestas condições o limite existirá .
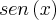 , tenho que: 2X²+aX-(a+2)=(2X+a+2)(X-1) (expressão 1)
, tenho que: 2X²+aX-(a+2)=(2X+a+2)(X-1) (expressão 1)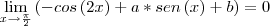 (equação 1)
(equação 1) ,
, 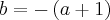 (equação 2)
(equação 2)
 =(2X+a+2)(X-1) (equação 3)
=(2X+a+2)(X-1) (equação 3)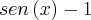 e
e 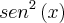 -1=
-1=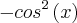 e
e 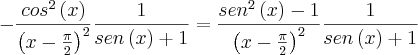
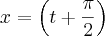 (equação 4),
(equação 4),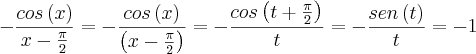
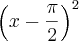 ]*
]*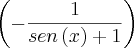
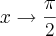 , portanto a=-4 e b=3.
, portanto a=-4 e b=3.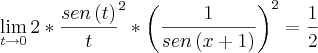 .
. e
e  . O valor do limite é
. O valor do limite é  .
.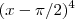 e não
e não 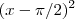 ,fazendo
,fazendo 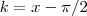 fica no denominador
fica no denominador 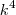 e não
e não 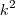 .Caso fosse
.Caso fosse 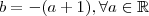 o limite sempre existiria, como mostra o wolframalpha :
o limite sempre existiria, como mostra o wolframalpha : 




