 por Erick » Sáb Mar 30, 2013 11:11
por Erick » Sáb Mar 30, 2013 11:11
Olá, segunda terei a 1°prova de calculo mas ainda tenho alguns problemas para resolve limites infinitos dentro de raizes, como por exemplo:
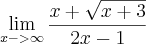
pois eu devo deixar o x em evidencia dentro ou fora da raiz? Se eu for deixar ele dentro da raiz, ao tirá-lo ficara x+(x^1/2)*1/(2x-1), e na resposta do livro esta dizendo q o resultado é 1/2. Como eu chego nisso?
Gostaria que pudessem me ajudar, pois n sei como posso resolver limites qnd esta dentro da raiz, sempre acabo me confundindo.
Grato desde ja
-
Erick
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mar 17, 2013 13:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Sáb Mar 30, 2013 12:05
por young_jedi » Sáb Mar 30, 2013 12:05
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- limites infinitos
por oleve » Qua Jan 21, 2009 18:15
- 1 Respostas
- 3026 Exibições
- Última mensagem por Sandra Piedade

Sáb Jan 24, 2009 22:30
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos
por Sobreira » Sáb Out 13, 2012 00:07
- 7 Respostas
- 4528 Exibições
- Última mensagem por MarceloFantini

Ter Out 30, 2012 09:07
Cálculo: Limites, Derivadas e Integrais
-
- Limites Infinitos. Ajuda
por valeuleo » Qua Jun 22, 2011 12:39
- 4 Respostas
- 3135 Exibições
- Última mensagem por renatav

Dom Jun 26, 2011 22:46
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos com modulo.
 por Sobreira » Sex Out 12, 2012 18:04
por Sobreira » Sex Out 12, 2012 18:04
- 13 Respostas
- 9043 Exibições
- Última mensagem por Sobreira

Sex Out 12, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limites infinitos envolvendo série
 por davifd_ » Ter Ago 18, 2015 15:56
por davifd_ » Ter Ago 18, 2015 15:56
- 10 Respostas
- 10659 Exibições
- Última mensagem por nakagumahissao

Qua Ago 19, 2015 09:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
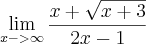 pois eu devo deixar o x em evidencia dentro ou fora da raiz? Se eu for deixar ele dentro da raiz, ao tirá-lo ficara x+(x^1/2)*1/(2x-1), e na resposta do livro esta dizendo q o resultado é 1/2. Como eu chego nisso?
pois eu devo deixar o x em evidencia dentro ou fora da raiz? Se eu for deixar ele dentro da raiz, ao tirá-lo ficara x+(x^1/2)*1/(2x-1), e na resposta do livro esta dizendo q o resultado é 1/2. Como eu chego nisso?

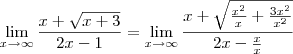
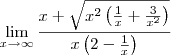
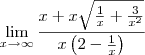
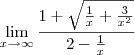
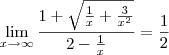


 .
.



