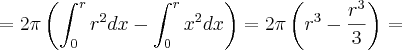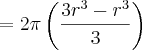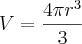[Integral] Volume de Esfera
Não sei deduzir esta fórmula... alguém pode ajudar?
O volume de um esfera de raio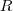 é dado por
é dado por 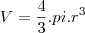 .
.
Com o estudo de integrais podemos provar que realmente esta fórmula do volume é verdadeira, basta pensar que uma esfera de raio R é gerada pela rotação em torno do eixo x da circunferência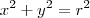 .
.
Sendo assim usando os conceitos de volume de sólido de revolução prove a fórmula do volume da esfera
O volume de um esfera de raio
 é dado por
é dado por 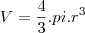 .
.Com o estudo de integrais podemos provar que realmente esta fórmula do volume é verdadeira, basta pensar que uma esfera de raio R é gerada pela rotação em torno do eixo x da circunferência
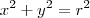 .
. Sendo assim usando os conceitos de volume de sólido de revolução prove a fórmula do volume da esfera
 .
. 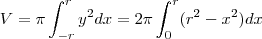
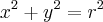
![y = \sqrt[]{r^{2} - x^{2}} y = \sqrt[]{r^{2} - x^{2}}](/latexrender/pictures/cd2d925abd7384eeabb03523959926e1.png) e x =[0, r]
e x =[0, r]![V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx = V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx =](/latexrender/pictures/c0a479dc9f74960a3d32e3005ceb5b24.png)