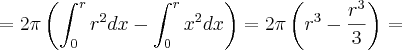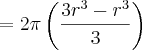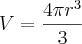-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480242 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 539755 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 503628 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 728093 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2164803 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por klueger » Ter Mar 19, 2013 13:58
por klueger » Ter Mar 19, 2013 13:58
Não sei deduzir esta fórmula... alguém pode ajudar?
O volume de um esfera de raio
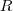
é dado por
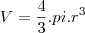
.
Com o estudo de integrais podemos provar que realmente esta fórmula do volume é verdadeira, basta pensar que uma esfera de raio R é gerada pela rotação em torno do eixo x da circunferência
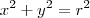
.
Sendo assim usando os conceitos de volume de sólido de revolução
prove a fórmula do volume da esfera
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Ter Mar 19, 2013 17:06
por e8group » Ter Mar 19, 2013 17:06
Solução :

.
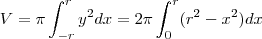
Tente concluir ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por nakagumahissao » Ter Mar 19, 2013 17:13
por nakagumahissao » Ter Mar 19, 2013 17:13
Resolução:
Demonstração:
Considere uma circunferência definida por:
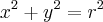
Considere ainda, que iremos 'rotacionar' em torno do eixo x apenas a parte do círculo situada no primeiro quadrante do gráfico, ou seja:
![y = \sqrt[]{r^{2} - x^{2}} y = \sqrt[]{r^{2} - x^{2}}](/latexrender/pictures/cd2d925abd7384eeabb03523959926e1.png)
e x =[0, r]
Como rotacionaremos apenas a parte do círculo do nosso primeiro quadrante, após termos calculado o volume da figura rotacionada no gráfico, teremos então que multiplicá-lo por 2 para termos o volume total. Desta maneira:
![V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx = V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx =](/latexrender/pictures/c0a479dc9f74960a3d32e3005ceb5b24.png)
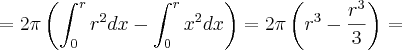
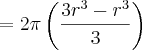
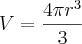
Como queríamos demonstrar.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- O volume de uma esfera em relação a outra esfera
por Macedo Junior » Sáb Jul 23, 2016 21:01
- 2 Respostas
- 8929 Exibições
- Última mensagem por Macedo Junior

Sáb Jul 23, 2016 23:28
Geometria Plana
-
- Fórmula de volume de uma esfera
por Kelvin Brayan » Dom Mai 01, 2011 21:10
- 2 Respostas
- 3174 Exibições
- Última mensagem por Kelvin Brayan

Dom Mai 01, 2011 21:37
Álgebra Elementar
-
- Volume do cilindro e da esfera
por Pri Ferreira » Sex Mai 18, 2012 23:24
- 0 Respostas
- 2083 Exibições
- Última mensagem por Pri Ferreira

Sex Mai 18, 2012 23:24
Geometria Espacial
-
- [Cálculo do volume da esfera (coordenadas esféricas)]
por Horus123 » Qua Out 19, 2016 14:56
- 0 Respostas
- 4611 Exibições
- Última mensagem por Horus123

Qua Out 19, 2016 14:56
Cálculo: Limites, Derivadas e Integrais
-
- Por que a derivada do volume de uma esfera é igual a área?
por Therodrigou » Ter Abr 09, 2019 05:30
- 3 Respostas
- 13092 Exibições
- Última mensagem por Therodrigou

Ter Mai 05, 2020 04:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 40 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
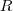 é dado por
é dado por 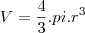 .
.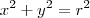 .
. 

 .
. 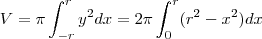

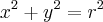
![y = \sqrt[]{r^{2} - x^{2}} y = \sqrt[]{r^{2} - x^{2}}](/latexrender/pictures/cd2d925abd7384eeabb03523959926e1.png) e x =[0, r]
e x =[0, r]![V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx = V = 2\pi\int_{0}^{r} \left[\sqrt[]{r^{2} - x^{2}} \right]^{2} dx = 2\pi\int_{0}^{r} r^{2} - x^{2} dx =](/latexrender/pictures/c0a479dc9f74960a3d32e3005ceb5b24.png)