-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478706 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534778 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498376 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 714229 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2136538 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Matheus Lacombe O » Sáb Mar 02, 2013 23:54
por Matheus Lacombe O » Sáb Mar 02, 2013 23:54
- Olá pessoal! Cá estou eu, mais uma vez. Pois bem. Tenho uma lista com setenta exercícios do livro
Calculo(Howard Anton) para resolver. Resolvi sem problema os primeiros exercícios, porém, chegando ao nº6 encontrei uma dificuldade que parece ser comum a todos os itens deste exercício: depois de aplicar a substituição eu termino com uma expressão onde não consigo mais integrar, pois não é possível "trazer o denominador para cima".
nº6) Item c)
![\int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx \int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx](/latexrender/pictures/c1118fa067dab539f80f68636b31fa7f.png)
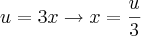

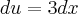
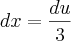
![\int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3} \int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3}](/latexrender/pictures/0dc0be322fd299ad9c298f433fc3dc80.png)
![\int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3} \int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3}](/latexrender/pictures/fce6437d1c4095b39b5eda37c3a9ccc7.png)
![\int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du \int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du](/latexrender/pictures/3e23f4a083f430fb38432bcca269ed0f.png)
- Paro nesta parte. Em suma, todos os itens do nº6 parecem dar neste mesmo problema. Eu não consigo tirar o
![u\sqrt[]{{u}^{2}-1} u\sqrt[]{{u}^{2}-1}](/latexrender/pictures/798b08b2792f6825aa0635f19f500ace.png)
do denominador e continuar.
Desde já grato pela atenção. Abraços.
Cordialmente, Matheus L. Oliveira.
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por e8group » Dom Mar 03, 2013 16:02
por e8group » Dom Mar 03, 2013 16:02
Boa tarde ,parece ser mais prático o desenvolvimento da questão caso faça a substituição

;daí derivando ambos membros em relação x ,obtemos :

.
Deste modo fazendo as devidas substiuições ,temos
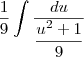
Consegue concluir ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Matheus Lacombe O » Dom Mar 03, 2013 17:19
por Matheus Lacombe O » Dom Mar 03, 2013 17:19
Sim, sim. O problema é que o exercício do Anton pede pro sujeito utilizar "u=3x". Dai da problema
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por e8group » Dom Mar 03, 2013 18:15
por e8group » Dom Mar 03, 2013 18:15
Ok.,neste caso recomendo que faça
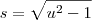
.Tente concluir .
OBS.: Veja que
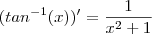
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral Indefinida] Método por Partes
por Matheus Lacombe O » Sex Mar 29, 2013 18:12
- 5 Respostas
- 2507 Exibições
- Última mensagem por young_jedi

Sáb Mar 30, 2013 21:33
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida (por substituição)
por Anne2011 » Sex Set 16, 2011 21:00
- 5 Respostas
- 2890 Exibições
- Última mensagem por Anne2011

Sex Set 16, 2011 21:47
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida (por substituição)
por Anne2011 » Sex Set 16, 2011 23:17
- 3 Respostas
- 2302 Exibições
- Última mensagem por MarceloFantini

Sáb Set 17, 2011 17:28
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Substituição
por fabriel » Qua Out 03, 2012 13:24
- 2 Respostas
- 1981 Exibições
- Última mensagem por fabriel

Qua Out 03, 2012 15:15
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL INDEFINIDA] Substituição
por fabriel » Seg Nov 26, 2012 00:03
- 4 Respostas
- 2847 Exibições
- Última mensagem por fabriel

Ter Nov 27, 2012 01:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 61 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx \int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx](/latexrender/pictures/c1118fa067dab539f80f68636b31fa7f.png)
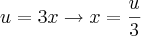

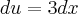
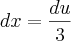
![\int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3} \int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3}](/latexrender/pictures/0dc0be322fd299ad9c298f433fc3dc80.png)
![\int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3} \int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3}](/latexrender/pictures/fce6437d1c4095b39b5eda37c3a9ccc7.png)
![\int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du \int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du](/latexrender/pictures/3e23f4a083f430fb38432bcca269ed0f.png)
![u\sqrt[]{{u}^{2}-1} u\sqrt[]{{u}^{2}-1}](/latexrender/pictures/798b08b2792f6825aa0635f19f500ace.png) do denominador e continuar.
do denominador e continuar.
![\int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx \int_{}^{}\frac{1}{x\sqrt[]{9{x}^{2}-1}}dx](/latexrender/pictures/c1118fa067dab539f80f68636b31fa7f.png)
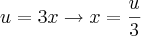

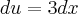
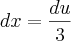
![\int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3} \int_{}^{}\frac{1}{\frac{u\sqrt[]{{u}^{2}-1}}{3}}.\frac{du}{3}](/latexrender/pictures/0dc0be322fd299ad9c298f433fc3dc80.png)
![\int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3} \int_{}^{}\frac{1}{1}.\frac{3}{u\sqrt[]{{u}^{2}-1}}.\frac{du}{3}](/latexrender/pictures/fce6437d1c4095b39b5eda37c3a9ccc7.png)
![\int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du \int_{}^{}\frac{1}{u\sqrt[]{{u}^{2}-1}}.du](/latexrender/pictures/3e23f4a083f430fb38432bcca269ed0f.png)
![u\sqrt[]{{u}^{2}-1} u\sqrt[]{{u}^{2}-1}](/latexrender/pictures/798b08b2792f6825aa0635f19f500ace.png) do denominador e continuar.
do denominador e continuar.
 ;daí derivando ambos membros em relação x ,obtemos :
;daí derivando ambos membros em relação x ,obtemos :  .
.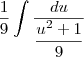


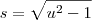 .Tente concluir .
.Tente concluir . 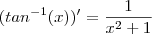 .
.





