 por Douglas16 » Qua Fev 27, 2013 20:38
por Douglas16 » Qua Fev 27, 2013 20:38
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Qua Fev 27, 2013 20:50
por Russman » Qua Fev 27, 2013 20:50
Sabe usa a L'Hopital?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Douglas16 » Qua Fev 27, 2013 21:11
por Douglas16 » Qua Fev 27, 2013 21:11
sei como usá-la, mas a resolução não deve usar a regra em si, no máximo somente os mesmos princípios de raciocínio mais básicos, mas não a regra de L' Hôpital.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Qua Fev 27, 2013 21:44
por Russman » Qua Fev 27, 2013 21:44
Então tente multiplicar o limite por
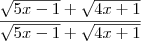
e , em seguida, por
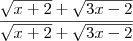
.
Lembre-se que o intuito disto vem do Produto Notável
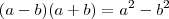
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Douglas16 » Qua Fev 27, 2013 22:08
por Douglas16 » Qua Fev 27, 2013 22:08
continua dando

que é indeterminado.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Qua Fev 27, 2013 23:07
por Russman » Qua Fev 27, 2013 23:07
Impossível.
Fazendo a 1° multiplicação você obtém
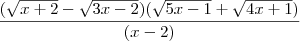
que ainda sim resulta indeterminado.
Fazendo a 2° multiplicação, então, chegamos em
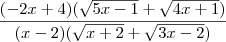
.
Observe que
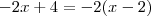
.
Tente continuar a partir daí.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Douglas16 » Qua Fev 27, 2013 23:17
por Douglas16 » Qua Fev 27, 2013 23:17
isso aí, correto.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolução de um limite de uma função (a solução é -1/2)
por Douglas16 » Qui Fev 28, 2013 12:30
- 1 Respostas
- 1051 Exibições
- Última mensagem por Jhonata

Qui Fev 28, 2013 13:41
Cálculo: Limites, Derivadas e Integrais
-
- Função inversa, Solução
por Deronsi » Ter Nov 06, 2012 00:29
- 4 Respostas
- 2200 Exibições
- Última mensagem por Deronsi

Ter Nov 06, 2012 08:08
Funções
-
- [Cálculo de Limite] Resolução de um limite
por julianocoutinho » Seg Mai 13, 2013 01:47
- 3 Respostas
- 3335 Exibições
- Última mensagem por Man Utd

Qua Mai 15, 2013 22:26
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO
por beel » Sex Set 02, 2011 15:14
- 2 Respostas
- 1719 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:03
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO 2
por beel » Sex Set 02, 2011 17:58
- 2 Respostas
- 1717 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow2}\frac{\sqrt[]{x+2}-\sqrt[]{3x-2}}{\sqrt[]{5x-1}-\sqrt[]{4x+1}} \lim_{x\rightarrow2}\frac{\sqrt[]{x+2}-\sqrt[]{3x-2}}{\sqrt[]{5x-1}-\sqrt[]{4x+1}}](/latexrender/pictures/1387df7c31d5dbade3fa7267fc7bfcaa.png)





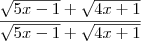
 .
.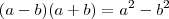

 que é indeterminado.
que é indeterminado.
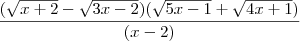
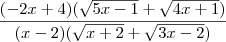 .
.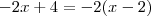 .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
