-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477985 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530304 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493881 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 701439 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2113737 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Jol » Ter Fev 26, 2013 19:33
por Jol » Ter Fev 26, 2013 19:33
Ola pessoal, sou novo aki, portanto ainda não sei bem como funciona! haha. Mas desde ja, agradeço pelo site, sei que é de grande utilidade!
Bom vamos a duvida...existem dois limites que estou tendo dificuldades de resolver, principalmente em começar!
Este é o primeiro: Penso eu que poderia fazer pelo metodo do fog: lim f(g(x)), tentei..mais nao deu certo!
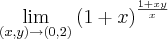
Este é o segundo: Tentei racionaliza-lo, só que ainda ano poderia substituir os valores, pois o denominador iria zerar!
![\lim_{(x,y)\rightarrow(1,1)}\frac{\sqrt[3]{xy}-1}{\sqrt[2]{xy}-1} \lim_{(x,y)\rightarrow(1,1)}\frac{\sqrt[3]{xy}-1}{\sqrt[2]{xy}-1}](/latexrender/pictures/e52beca78d7db3174492162f0133f2eb.png)
Desde ja, agradeço!
-
Jol
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Fev 26, 2013 19:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Qua Fev 27, 2013 18:43
por young_jedi » Qua Fev 27, 2013 18:43
neste primeiro voce pode fazer
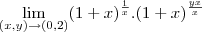
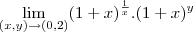
mais sabemos que

e
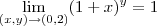
portanto
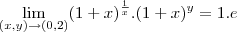
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites duas variaveis
por Razoli » Qui Jul 03, 2014 23:22
- 2 Respostas
- 2116 Exibições
- Última mensagem por Razoli

Qui Jul 03, 2014 23:41
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Função de duas variáveis
por Sohrab » Ter Abr 23, 2013 03:18
- 7 Respostas
- 5935 Exibições
- Última mensagem por brunno10

Qua Mai 01, 2013 00:28
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES função com duas variáveis, teo confronto
por inkz » Dom Nov 25, 2012 15:32
- 6 Respostas
- 8430 Exibições
- Última mensagem por e8group

Seg Nov 26, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Equação de limite de duas variáveis reais
por Bianca_R » Dom Nov 04, 2012 21:45
- 1 Respostas
- 1809 Exibições
- Última mensagem por e8group

Seg Nov 05, 2012 11:19
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] duas variáveis. Prova através da definição formal
por marcosmuscul » Sáb Jan 25, 2014 17:59
- 2 Respostas
- 5610 Exibições
- Última mensagem por marcosmuscul

Ter Fev 04, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 60 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
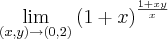
![\lim_{(x,y)\rightarrow(1,1)}\frac{\sqrt[3]{xy}-1}{\sqrt[2]{xy}-1} \lim_{(x,y)\rightarrow(1,1)}\frac{\sqrt[3]{xy}-1}{\sqrt[2]{xy}-1}](/latexrender/pictures/e52beca78d7db3174492162f0133f2eb.png)



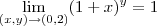
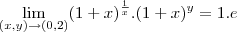



 , avisa que eu resolvo.
, avisa que eu resolvo.

