 por matmatco » Sáb Fev 23, 2013 16:35
por matmatco » Sáb Fev 23, 2013 16:35
![\lim_{x\to0}\left[\frac{1}{x}+lnx \right] \lim_{x\to0}\left[\frac{1}{x}+lnx \right]](/latexrender/pictures/2d844ef6ee435deda50470d8d9383b89.png)
, não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
alguém me ajude por favor
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por LuizAquino » Ter Fev 26, 2013 17:09
por LuizAquino » Ter Fev 26, 2013 17:09
matmatco escreveu:![\lim_{x\to0}\left[\frac{1}{x}+lnx \right] \lim_{x\to0}\left[\frac{1}{x}+lnx \right]](/latexrender/pictures/2d844ef6ee435deda50470d8d9383b89.png)
, não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
alguém me ajude por favor
Em primeiro lugar, vale destacar que este limite está mal definido. Isso porque para
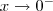
(e portanto x < 0), temos que
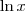
não está definido. O que podemos calcular na verdade é:
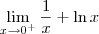
Feita esta observação, vejamos como começar o desenvolvimento desse limite.
Analisando este limite, note que temos uma indeterminação do tipo

. Para aplicar a Regra de L'Hospital, precisamos reescrever esse limite na forma
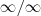
(ou ainda, 0/0).
Uma estratégia clássica nesse caso é fazer o seguinte:
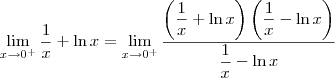
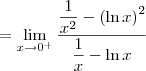
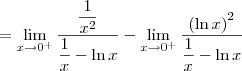
Note que agora cada um desses limites é do tipo
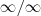
. Desse modo, podemos aplicar a Regra de L'Hospital em cada um deles.
Tente concluir o exercício a partir daí.
ObservaçãoCuidado para não confundir
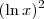
com
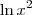
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- L'Hospital
por cal12 » Sáb Nov 26, 2011 17:52
- 1 Respostas
- 1683 Exibições
- Última mensagem por LuizAquino

Sáb Nov 26, 2011 18:13
Cálculo: Limites, Derivadas e Integrais
-
- l'hospital
por vinicastro » Dom Dez 16, 2012 16:32
- 1 Respostas
- 1521 Exibições
- Última mensagem por vinicastro

Dom Dez 16, 2012 17:15
Cálculo: Limites, Derivadas e Integrais
-
- L'Hospital
por duduxo81 » Sex Jul 08, 2016 11:30
- 3 Respostas
- 5278 Exibições
- Última mensagem por duduxo81

Qua Jul 13, 2016 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 20:26
- 2 Respostas
- 1919 Exibições
- Última mensagem por Claudin

Qui Jul 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 21:16
- 9 Respostas
- 3355 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 16, 2011 15:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\to0}\left[\frac{1}{x}+lnx \right] \lim_{x\to0}\left[\frac{1}{x}+lnx \right]](/latexrender/pictures/2d844ef6ee435deda50470d8d9383b89.png) , não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
, não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
![\lim_{x\to0}\left[\frac{1}{x}+lnx \right] \lim_{x\to0}\left[\frac{1}{x}+lnx \right]](/latexrender/pictures/2d844ef6ee435deda50470d8d9383b89.png) , não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
, não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
, não estou conseguindo resolver esse limite por l'hospital a resposta é infinito mas só encontro zero.
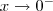 (e portanto x < 0), temos que
(e portanto x < 0), temos que 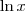 não está definido. O que podemos calcular na verdade é:
não está definido. O que podemos calcular na verdade é: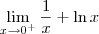
 . Para aplicar a Regra de L'Hospital, precisamos reescrever esse limite na forma
. Para aplicar a Regra de L'Hospital, precisamos reescrever esse limite na forma 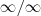 (ou ainda, 0/0).
(ou ainda, 0/0).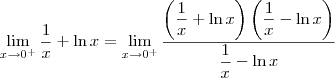
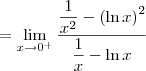
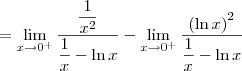
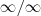 . Desse modo, podemos aplicar a Regra de L'Hospital em cada um deles.
. Desse modo, podemos aplicar a Regra de L'Hospital em cada um deles.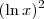 com
com 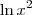 .
.