 por menino de ouro » Qua Jan 23, 2013 00:03
por menino de ouro » Qua Jan 23, 2013 00:03
pessoal ,
nessa questão, como desenrolar as contas , não sei coma analisar?
![\lim_{x\rightarrow \infty}\frac{\sqrt[]{9x^2+x}}{x+8}=3 \lim_{x\rightarrow \infty}\frac{\sqrt[]{9x^2+x}}{x+8}=3](/latexrender/pictures/931233037b0ca8ced29c46fa8ae03b95.png)
por que da 3?
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por young_jedi » Qua Jan 23, 2013 11:30
por young_jedi » Qua Jan 23, 2013 11:30
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por menino de ouro » Qua Jan 23, 2013 12:12
por menino de ouro » Qua Jan 23, 2013 12:12
no

, dentro da raiz quando passa multiplicando , me parece que ta faltando um x?
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por young_jedi » Qua Jan 23, 2013 14:52
por young_jedi » Qua Jan 23, 2013 14:52
conferi e não encontrei nenhume erro, acho que não entendi sua duvida
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por menino de ouro » Qua Jan 23, 2013 15:52
por menino de ouro » Qua Jan 23, 2013 15:52
na terceira para quarta etapa da resolução,
tem -se

, você colocou um x para fora da raiz quadrada , multiplicando toda raiz , no caso onde foi parar o outro x
-
menino de ouro
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Out 23, 2012 22:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por e8group » Qua Jan 23, 2013 17:15
por e8group » Qua Jan 23, 2013 17:15
Basta notar que devido a propriedade

fazendo

e
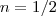
. Em consequência disto ,
![\sqrt{x^2(9+1/x)} = \left[x^2(9+1/x)\right]^{1/2} = (x^2)^{1/2} \cdot (9+1/x)^{1/2} = \sqrt{x^2} \cdot \sqrt{9+1/x} = x \cdot \sqrt{9+1/x} \sqrt{x^2(9+1/x)} = \left[x^2(9+1/x)\right]^{1/2} = (x^2)^{1/2} \cdot (9+1/x)^{1/2} = \sqrt{x^2} \cdot \sqrt{9+1/x} = x \cdot \sqrt{9+1/x}](/latexrender/pictures/22c3401f77df62f0e3cf1d0d2b83e695.png)
(x \geq 0 )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3534 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- Limites no Infinito - Encontre r > 0 para um dado épsilon
por elisafrombrazil » Sáb Jan 21, 2017 10:35
- 1 Respostas
- 4154 Exibições
- Última mensagem por e8group

Qui Fev 02, 2017 15:59
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7266 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Questão de limite tendendo à infinito
por _bruno94 » Sex Mai 31, 2013 00:28
- 3 Respostas
- 2947 Exibições
- Última mensagem por Jhonata

Sex Mai 31, 2013 01:30
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Limite que tende ao infinito
por Mell » Qua Mai 08, 2013 00:09
- 3 Respostas
- 2637 Exibições
- Última mensagem por e8group

Qua Mai 08, 2013 21:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow \infty}\frac{\sqrt[]{9x^2+x}}{x+8}=3 \lim_{x\rightarrow \infty}\frac{\sqrt[]{9x^2+x}}{x+8}=3](/latexrender/pictures/931233037b0ca8ced29c46fa8ae03b95.png)

![\lim_{x\rightarrow \infty}\frac{\sqrt[]{9x^2+x}}{x+8}=3 \lim_{x\rightarrow \infty}\frac{\sqrt[]{9x^2+x}}{x+8}=3](/latexrender/pictures/931233037b0ca8ced29c46fa8ae03b95.png)

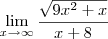

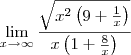

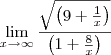


 , dentro da raiz quando passa multiplicando , me parece que ta faltando um x?
, dentro da raiz quando passa multiplicando , me parece que ta faltando um x?

 , você colocou um x para fora da raiz quadrada , multiplicando toda raiz , no caso onde foi parar o outro x
, você colocou um x para fora da raiz quadrada , multiplicando toda raiz , no caso onde foi parar o outro x
 fazendo
fazendo  e
e 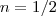 . Em consequência disto ,
. Em consequência disto ,![\sqrt{x^2(9+1/x)} = \left[x^2(9+1/x)\right]^{1/2} = (x^2)^{1/2} \cdot (9+1/x)^{1/2} = \sqrt{x^2} \cdot \sqrt{9+1/x} = x \cdot \sqrt{9+1/x} \sqrt{x^2(9+1/x)} = \left[x^2(9+1/x)\right]^{1/2} = (x^2)^{1/2} \cdot (9+1/x)^{1/2} = \sqrt{x^2} \cdot \sqrt{9+1/x} = x \cdot \sqrt{9+1/x}](/latexrender/pictures/22c3401f77df62f0e3cf1d0d2b83e695.png) (x \geq 0 )
(x \geq 0 )
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.