 por Marlon Teofilo » Ter Jan 22, 2013 14:23
por Marlon Teofilo » Ter Jan 22, 2013 14:23
Oi boa tarde.
Estou com dificuldades em resolver um limite.
é o seguinte:
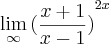
entao, iniciei separando em duas frações, ambas com demoninador (x-1), fazendo os limites separados.
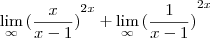
O segundo termo cheguei à conclusão que é 1/infinito=0
O primeiro termo conclui que a resposta do limite é e^2, após mudar a base e todo aquele processo de sempre, hehehehe, gostaria de saber se está correto, pois desconfio que não! kkkkkkkk
-
Marlon Teofilo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jan 07, 2013 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por e8group » Ter Jan 22, 2013 17:43
por e8group » Ter Jan 22, 2013 17:43
Cuidado!
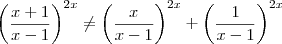
Como dica note que ,
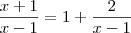
.
Logo ,
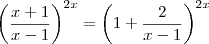
e portanto ,
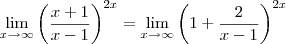
.
Além disso , tomando
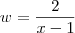
.Quando
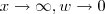
.Fazendo as substituições ,
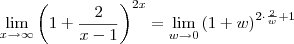
Usando as propriedades
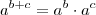
e
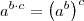
e também dos limites, uma delas do produto .
Segue então :
![\lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4 \lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4](/latexrender/pictures/0e2d8979072ad1690fa73549a2250b33.png)
.
Obs.: Para compreender a resolução veja os limites fundamentais em especial o limite fundamental que denomina-se o número Euler . Para ler mais ,
http://pt.wikipedia.org/wiki/N%C3%BAmero_de_Euler .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Marlon Teofilo » Ter Jan 22, 2013 18:01
por Marlon Teofilo » Ter Jan 22, 2013 18:01
Obrigado, minha duvida realmente era se eu utilizei a propriedade de forma correta, e errei hehehehe
vlw mano, entendi!!!
-
Marlon Teofilo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Jan 07, 2013 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por lyppeferreira_ » Sáb Abr 04, 2020 15:33
por lyppeferreira_ » Sáb Abr 04, 2020 15:33
e8group escreveu:Cuidado!
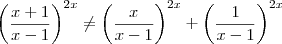
Como dica note que ,
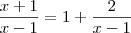
.
Logo ,
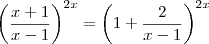
e portanto ,
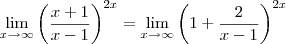
.
Além disso , tomando
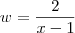
.Quando
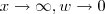
.Fazendo as substituições ,
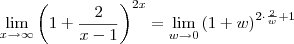
Usando as propriedades
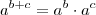
e
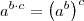
e também dos limites, uma delas do produto .
Segue então :
![\lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4 \lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4](/latexrender/pictures/0e2d8979072ad1690fa73549a2250b33.png)
.
Obs.: Para compreender a resolução veja os limites fundamentais em especial o limite fundamental que denomina-se o número Euler . Para ler mais ,
http://pt.wikipedia.org/wiki/N%C3%BAmero_de_Euler .
Como você chegou nessa
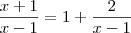
Tô travado nessa passagem. Eu tentei pela propriedade do quociente dos limites, mas não cheguei nesse resultado que vc conseguiu.
-
lyppeferreira_
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 04, 2020 08:03
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por adauto martins » Dom Abr 05, 2020 11:20
por adauto martins » Dom Abr 05, 2020 11:20
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites de função exponencial
por Silas » Qui Jul 10, 2014 18:12
- 2 Respostas
- 2147 Exibições
- Última mensagem por Silas

Qui Jul 10, 2014 21:47
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Limite fundamental Exponencial
por antonelli2006 » Ter Set 20, 2011 05:54
- 1 Respostas
- 2031 Exibições
- Última mensagem por LuizAquino

Ter Set 20, 2011 12:22
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda sobre Limites seno e exponencial
por gn66 » Sex Jun 03, 2011 12:02
- 8 Respostas
- 5082 Exibições
- Última mensagem por gn66

Sex Jun 03, 2011 16:34
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4751 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
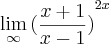
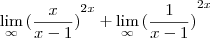


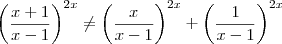
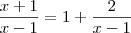 .
.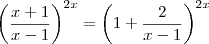
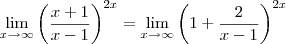 .
. 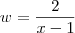 .Quando
.Quando 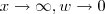 .Fazendo as substituições ,
.Fazendo as substituições , 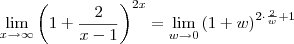
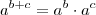 e
e 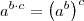 e também dos limites, uma delas do produto .
e também dos limites, uma delas do produto . ![\lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4 \lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4](/latexrender/pictures/0e2d8979072ad1690fa73549a2250b33.png) .
. 
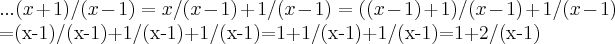


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.