-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478194 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532073 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495601 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 706444 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2122866 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Matheus Lacombe O » Ter Dez 11, 2012 23:46
por Matheus Lacombe O » Ter Dez 11, 2012 23:46
-
Matheus Lacombe O
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Jun 03, 2011 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Mecânica
- Andamento: cursando
 por Russman » Qua Dez 12, 2012 01:39
por Russman » Qua Dez 12, 2012 01:39
Repare que a sua função é do tipo
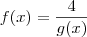
.
Assim, podemos derivá-la usando a Regra do Quociente. Esta diz que :
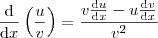
Tomando

e
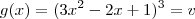
, temos:
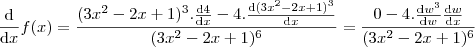
Tomei
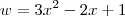
para aplicar a regra da cadeia e o zero que surge vem de
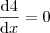
.
Agora, continuando:
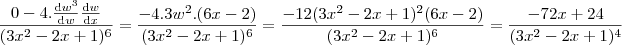
Chegamos a resposta!
Se formos fazer por regra do produto, então
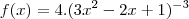
e como
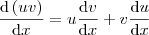
então tomando

e
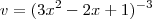
temos:
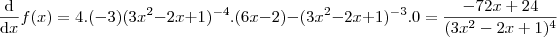
pois
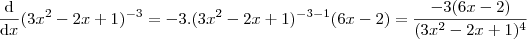
.
Mas agora veja que como a primeira função,

, é constante bastava apenas que você usasse a propriedade
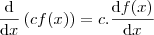
, isto é, "a constante sai fora da derivada"!. Tente fazer assim e veja se chega no mesmo resultado!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada- Como aplicar as formulas do quociente e do produto
por karinak » Sáb Jun 16, 2012 02:08
- 2 Respostas
- 1589 Exibições
- Última mensagem por karinak

Sáb Jun 16, 2012 12:43
Cálculo: Limites, Derivadas e Integrais
-
- inequação produto/quociente
por vhcs29 » Qui Abr 01, 2010 12:32
- 2 Respostas
- 4960 Exibições
- Última mensagem por vhcs29

Sex Abr 02, 2010 12:59
Álgebra Elementar
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 9789 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida para achar quociente das diferenças da função
por gabrielajax » Qui Mar 19, 2015 12:11
- 2 Respostas
- 12397 Exibições
- Última mensagem por gabrielajax

Sex Mar 20, 2015 10:42
Funções
-
- Derivada do Quociente
 por dekol2 » Dom Mai 06, 2012 20:39
por dekol2 » Dom Mai 06, 2012 20:39
- 4 Respostas
- 2870 Exibições
- Última mensagem por LuizAquino

Seg Mai 07, 2012 11:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 110 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
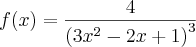
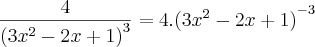

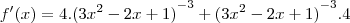
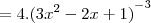
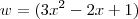
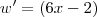
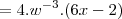
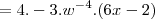
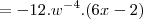
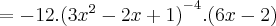

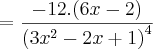
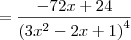 - O que bate com a resposta do Microsoft Mathematics.
- O que bate com a resposta do Microsoft Mathematics.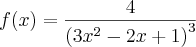
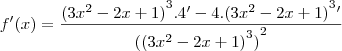
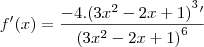
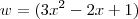
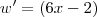
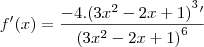
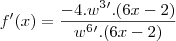
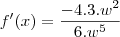
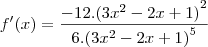
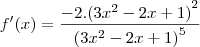
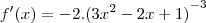
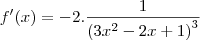
 - O que não bate nem com a resposta do Microsoft Mathematics, nem com a do gabarito.
- O que não bate nem com a resposta do Microsoft Mathematics, nem com a do gabarito.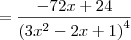 (Microsoft Mathematics) ou
(Microsoft Mathematics) ou![\frac{24(1-3x)}{4\sqrt[]{x}.\sqrt[]{4+3}.\sqrt[]{x}} \frac{24(1-3x)}{4\sqrt[]{x}.\sqrt[]{4+3}.\sqrt[]{x}}](/latexrender/pictures/e0edd6ef95ba1061f726eb7f7193882c.png) (Professor)
(Professor)

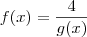 .
.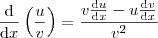
 e
e 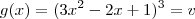 , temos:
, temos: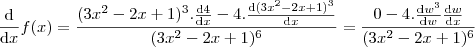
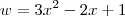 para aplicar a regra da cadeia e o zero que surge vem de
para aplicar a regra da cadeia e o zero que surge vem de 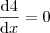 .
.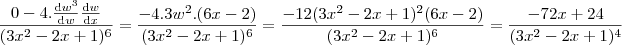
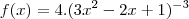 e como
e como 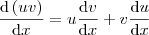 então tomando
então tomando 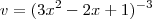 temos:
temos: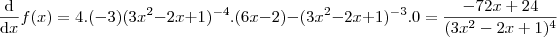
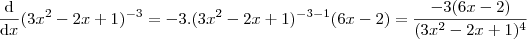 .
.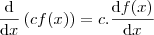 , isto é, "a constante sai fora da derivada"!. Tente fazer assim e veja se chega no mesmo resultado!
, isto é, "a constante sai fora da derivada"!. Tente fazer assim e veja se chega no mesmo resultado!





