tenho um trabalho para desenvolver, que preciso calcular determinadas coisas solicitadas no software "Máxima"
a partir da expressão:
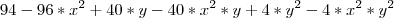.É pedido que se calcule:
1 - Os pontos críticos.
2 - Classificar os pontos críticos;
3. No domínio que contenha os pontos críticos, determinar em gráficos distintos:
3.1. O gráfico da superfície;
3.2. O mapa das curvas de nível;
3.3. O campo gradiente;
3.4. Sobrepor o mapa das curvas de nível com o campo gradiente;
3.5. Determinar os pontos de máximo e mínimo absolutos e o valor que a função assume nesses pontos;
3.6. Determinar um plano tangente a um ponto P da superfície a sua escolha, que não seja crítico.
Nunca usei o Máxima e estou "apanhando" para entender e aprender.
Já consegui calcular os pontos críticos, e depois disso, fiz a matriz hessiana.
Mas a primeira dúvida vem aí. Eu não sei o que eu posso gerar a partir da determinante da matriz hessiana.
O professor pediu que pesquisássemos, mas tudo que pesquisei é muito vago e não consigo assimilar com o trabalho.
Preciso muito de ajuda!!!
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.