-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477971 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 530212 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493799 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 701185 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2113282 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Dan » Seg Set 14, 2009 09:52
por Dan » Seg Set 14, 2009 09:52
Olá gente! Não estou conseguindo resolver a seguinte
integral:
![\int_{1}^{5}x.\sqrt[]{x-1}.dx \int_{1}^{5}x.\sqrt[]{x-1}.dx](/latexrender/pictures/cb1cc53b22d166760056542a5302cd63.png)
Tentei fazer por
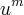
, e como a derivada do que está dentro da raíz é igual a 1, falta um x para cortar.
Alguém poderia me ajudar?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Elcioschin » Seg Set 14, 2009 11:27
por Elcioschin » Seg Set 14, 2009 11:27
Fazendo u = x - 1 temos:
x = u + 1
dx = du
V(x - 1) = (x - 1)^(1/2) = u^(1/2)
x*V(x -1) = (u + 1)*u^(1/2) = u^(3/2) + u^(1/2)
Integrando, obtém-se ----> (2/5)*u^(5/2) + (2/3)*u^(3/2)
Sunstituindo u ----> (2/5)*(x - 1)^(5/2) - (2/3)(x - 1)^(3/2)
Limite superior 5 -----> (2/5)*4^(5/2) - (2/3)*4^(3/2) = (2/5)*32 - (2/3)*8 = 64/5 - 16/3 = 112/15
Limite inferior 1 -----> 0
Solução ----> 112/15
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Dan » Seg Set 14, 2009 11:38
por Dan » Seg Set 14, 2009 11:38
Obrigado, Elcioschin.
Infelizmente ainda não aprendi substituição ou integral por partes pois só comecei com as integrais definidas semana passada.
Ficou confuso.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Dan » Ter Set 15, 2009 12:38
por Dan » Ter Set 15, 2009 12:38
De qualquer forma eu ainda vou aprender isso na faculdade. Era apenas curiosidade. Já conversei com uma amiga minha que é profe de matemática e ela me explicou.
Elcioschin, não quero que leve a mal o que vou te dizer, mas eu acho que não basta mostrar que você sabe fazer os problemas se as outras pessoas continuam com dúvidas. Quando eu entrei nesse fórum, apareceu uma janela que falava em interação. A interação deve existir por parte de quem responde também.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Dan » Ter Set 15, 2009 18:07
por Dan » Ter Set 15, 2009 18:07
Ah, e só pra constar...
No livro a resposta é
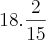
.
Tem certeza que a sua resposta está certa?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Elcioschin » Ter Set 15, 2009 23:54
por Elcioschin » Ter Set 15, 2009 23:54
Dan
Respondendo suas dúvidas e questionamentos:
1) A substituição que eu fiz foi muito bem explicada. Não sei porque você disse que "ficou confuso".
2) A partir da substituição a integração é bem básica, exatamente como você disse que tentou com u^m: Note que temos duas integrais: u^(3/2) e u^(1/2).
3) Quanto à minha solução, houve apenas uma troca de sinal na penúltima e última linha. Vou mostrar abaixo e editar em vermelho no original:
Integrando, obtém-se ----> (2/5)*u^(5/2) + (2/3)*u^(3/2)
Substituindo u ----> (2/5)*(x - 1)^(5/2) + (2/3)(x - 1)^(3/2)
Limite superior 5 -----> (2/5)*4^(5/2) + (2/3)*4^(3/2) = (2/5)*32 + (2/3)*8 = 64/5 + 16/3 = 272/15 = 18 2/15
Limite inferior ----> 0
Solução ----> 18 2/15
4) Não entendío motivo de você dizer que eu não estou interagindo:
a) Você postou a questão no dia 14/09 às 08:52
b) Eu respondí a questão no MESMO dia às 10:27
c) No mesmo dia você enviou uma resposta às 10:32
d) No dia 15 você manda nova mensagem às 11:38, SEM AGUARDAR uma resposta minha.
Acho que você deve imaginar que eu fico integralmente no computador aguardando as suas mensagens.
Porém, não é o que acontece: além de trabalhar e de ter outras ocupações, eu participo também de outros dois foruns.
Assim, não acho justa a sua reclamação. Espero que, da próxima vez, você tenha um pouco mais de paciência.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Dan » Qua Set 16, 2009 08:58
por Dan » Qua Set 16, 2009 08:58
Olá Elcioschin.
Não, não espero que você fique a meu serviço respondendo todas as minhas dúvidas. Aliás, agradeço a sua participação e sei que você fez tudo de boa fé.
Acontece que você, engenheiro formado, talvez não compreenda as dúvidas de um estudante de primeiro ano de faculdade. Eu estou começando a aprender integrais. O que para você é uma explicação completa, ficou bastante vago para mim. Aprendi poucos métodos, poucas coisas, e eu ainda não consegui compreender por que essa integral é resolvida dessa maneira, pelo menos pela sua explicação.
Você poderia ter me explicado o que é o "u" e o que é o "v" na sua maneira de resolver. É óbvio para você? Mas não para mim! É nisso que eu falo quando eu me refiro à interação. Você soube resolver muito bem a integral, mas infelizmente não conseguiu passar esse conhecimento para quem estava com a dúvida.
De qualquer forma, muito obrigado por responder à minha dúvida. Eu também poderia ter explicado melhor que pontos ficaram confusos na sua explicação.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 3552 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 3916 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 3718 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2305 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2363 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{1}^{5}x.\sqrt[]{x-1}.dx \int_{1}^{5}x.\sqrt[]{x-1}.dx](/latexrender/pictures/cb1cc53b22d166760056542a5302cd63.png)
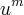 , e como a derivada do que está dentro da raíz é igual a 1, falta um x para cortar.
, e como a derivada do que está dentro da raíz é igual a 1, falta um x para cortar.
![\int_{1}^{5}x.\sqrt[]{x-1}.dx \int_{1}^{5}x.\sqrt[]{x-1}.dx](/latexrender/pictures/cb1cc53b22d166760056542a5302cd63.png)
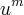 , e como a derivada do que está dentro da raíz é igual a 1, falta um x para cortar.
, e como a derivada do que está dentro da raíz é igual a 1, falta um x para cortar.



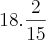 .
.



 .
.



