Mostre que s e f for uma função continua [a,b] então
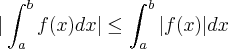
Sugestão:
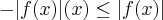
Use o exercicio anterior e prove também que
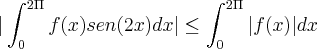
Não nem como começar em ambos os exercícios.

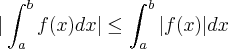
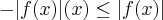
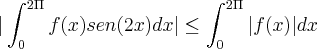

Claudin escreveu:Não sei como resolver o seguinte exercicio
Mostre que s e f for uma função continua [a,b] então
Sugestão:
Use o exercicio anterior e prove também que
Não nem como começar em ambos os exercícios.
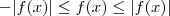
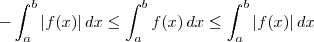
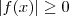
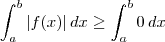
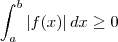
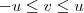 e
e 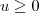 , então
, então  . Usando esse conhecimento com
. Usando esse conhecimento com 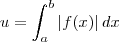 e
e 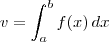 , concluímos que:
, concluímos que: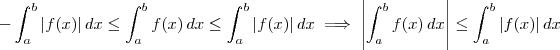
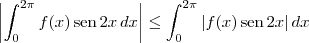

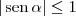 para qualquer ângulo
para qualquer ângulo  .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 23 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

