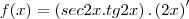por Sobreira » Ter Nov 27, 2012 16:38
por Sobreira » Ter Nov 27, 2012 16:38
Quando eu tenho uma função deste tipo:

Eu sei que o resultado é este:
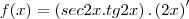
Agora quando eu tenho:


Eu gostaria de saber se eu estou calculando (de forma implícita o valor de

que vai dar 1, ou seja,

) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Ter Nov 27, 2012 19:36
por MarceloFantini » Ter Nov 27, 2012 19:36
Você está obtendo direto o resultado da derivada. Eu já pensei nisso, e a conclusão é que se pensarmos que estamos derivando implicitamente

este raciocínio não pára, de tal forma que toda derivada seria zero, pois você derivaria uma constante sempre no final.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Ter Nov 27, 2012 22:25
por Sobreira » Ter Nov 27, 2012 22:25
Uma outra coisa que eu pensei também é o seguinte (não sei se está correto) no primeiro caso eu tenho uma função composta e então eu aplico a regra da cadeia:

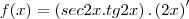
Já no segundo caso como eu tenho uma função "simples":

Não sei se posso aplicar a regra da cadeia também!!
O que acha??
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Ter Nov 27, 2012 22:27
por MarceloFantini » Ter Nov 27, 2012 22:27
Sim, você está correto: aplicamos a regra da cadeia apenas em funções compostas. A segunda função é elementar, portanto você já conhece sua derivada. Não existe regra da cadeia.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10886 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- Demonstração- secante
 por mathsoliver » Seg Abr 13, 2015 12:32
por mathsoliver » Seg Abr 13, 2015 12:32
- 1 Respostas
- 1759 Exibições
- Última mensagem por Cleyson007

Seg Abr 13, 2015 16:51
Equações
-
- seno e secante negativa
por Apotema » Seg Nov 23, 2009 14:36
- 2 Respostas
- 1991 Exibições
- Última mensagem por Apotema

Qua Nov 25, 2009 16:54
Trigonometria
-
- Função Secante e Cossecante
por gustavoluiss » Qui Jul 14, 2011 20:42
- 11 Respostas
- 5518 Exibições
- Última mensagem por gustavoluiss

Sáb Jul 16, 2011 15:19
Trigonometria
-
- [Cálculo] Integral da secante
por ARCS » Ter Ago 23, 2011 18:15
- 2 Respostas
- 8151 Exibições
- Última mensagem por LuizAquino

Ter Ago 23, 2011 23:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

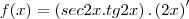


 que vai dar 1, ou seja,
que vai dar 1, ou seja,  ) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.

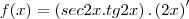


 que vai dar 1, ou seja,
que vai dar 1, ou seja,  ) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
) ou simplesmente não estou calculando o valor da derivada de x e obtendo direto o resultado.
 este raciocínio não pára, de tal forma que toda derivada seria zero, pois você derivaria uma constante sempre no final.
este raciocínio não pára, de tal forma que toda derivada seria zero, pois você derivaria uma constante sempre no final.