 E
E 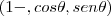 SE INTERSECTAM NO PONTO (1,1,0). DETERMINE AS EQUAÇÕES DAS RETAS TANGENTES ÀS CURVAS EM (1,1,0) E VERIFIQUE QUE ELAS SÃO ORTOGONAIS.
SE INTERSECTAM NO PONTO (1,1,0). DETERMINE AS EQUAÇÕES DAS RETAS TANGENTES ÀS CURVAS EM (1,1,0) E VERIFIQUE QUE ELAS SÃO ORTOGONAIS.Não consegui mostrar que elas se intersectam neste ponto.. alguém poderia me auxiliar?
Quanto ao resto do exercício, basta eu encontrar suas derivadas no ponto e verificar se o produto escalar entre elas é nulo?
Desde já, agradeço as respostas!!


 nas duas curvas. Então na primeira você terá
nas duas curvas. Então na primeira você terá 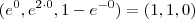 , enquanto que na segunda terá
, enquanto que na segunda terá 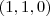 . Logo elas se interseccionam em
. Logo elas se interseccionam em 


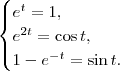


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)