 por inkz » Ter Nov 20, 2012 01:24
por inkz » Ter Nov 20, 2012 01:24
UMA PARTICULA MOVE-SE NO PLANO DE TAL FORMA QUE SUA POSIÇÃO NO INSTANTE
t É DADA POR:
C(t) =
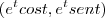
DEMONSTRE QUE O VETOR TANGENTE À TRAJETÓRIA FAZ UM ÂNGULO CONSTANTE DE pi/4 COM O VETOR POSIÇÃO.
Minha tentativa:Sei que o vetor tangente a trajetória é a derivada de C(t), então foi o que fiz, chegando em:
C'(t) =
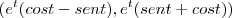
Tenho então o vetor tangente a trajetória. Agora como provo que o angulo entre ele e o vetor posição é pi/4??
Desde já, agradeço!!

-
inkz
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Nov 20, 2012 01:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por MarceloFantini » Ter Nov 20, 2012 01:41
por MarceloFantini » Ter Nov 20, 2012 01:41
Lembre-se que pelo produto escalar sabemos que

,
ou seja, o ângulo entre dois vetores é igual ao seu produto escalar dividido pelo produto das normas.
Neste caso, temos que a norma de
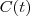
é
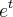
. Calcule
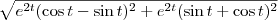
e

,
que são a norma de
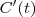
e o produto escalar
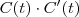
respectivamente, e substitua na equação.
Ao simplificar as contas o resultado deve ser
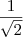
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por inkz » Ter Nov 20, 2012 01:55
por inkz » Ter Nov 20, 2012 01:55
MarceloFantini, primeiramente, gostaria de agradecer pela resposta.
Eu pensei exatamente em fazer isso, mas veja, todas as componentes de C e de C' estão em função de t, ou seja, não tem valor numérico.. como pode então essa simplificação terminar em um valor numérico?
-
inkz
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Nov 20, 2012 01:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por MarceloFantini » Ter Nov 20, 2012 02:10
por MarceloFantini » Ter Nov 20, 2012 02:10
Note que
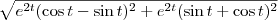

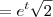
,
logo
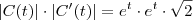
.
Na segunda conta temos

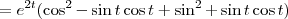
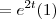
.
Portanto,
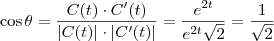
.
Bastava você ter expandido e simplificado. É falta de hábito mesmo, não é tão difícil.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por inkz » Ter Nov 20, 2012 02:13
por inkz » Ter Nov 20, 2012 02:13
de fato!!
vou terminar um exercício que estou fazendo aqui e refazer todos estes que postei aqui, em todas suas minúcias.
muito obrigado pela ajuda!!

-
inkz
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Nov 20, 2012 01:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por LuannLuna » Qui Nov 29, 2012 15:05
por LuannLuna » Qui Nov 29, 2012 15:05
Putz!... vlwzão!..
tava qbrando a cabeça nessa poha! aksdpoakpo =P
-
LuannLuna
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Nov 29, 2012 14:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Curvas] Encontrar o vetor posição dado vetor aceleração
 por amigao » Sex Mai 09, 2014 16:37
por amigao » Sex Mai 09, 2014 16:37
- 1 Respostas
- 2086 Exibições
- Última mensagem por Russman

Sex Mai 09, 2014 17:25
Geometria Analítica
-
- Vetor de posição polar
por Jhenrique » Seg Nov 11, 2013 20:23
- 0 Respostas
- 1079 Exibições
- Última mensagem por Jhenrique

Seg Nov 11, 2013 20:23
Geometria Analítica
-
- posição relativa entre os planos
por Ana Maria da Silva » Ter Jun 04, 2013 10:38
- 2 Respostas
- 3567 Exibições
- Última mensagem por Ana Maria da Silva

Ter Jun 04, 2013 20:31
Geometria Analítica
-
- posição relativa entre as retas r e pi
por Ana Maria da Silva » Qua Jun 05, 2013 11:55
- 0 Respostas
- 1346 Exibições
- Última mensagem por Ana Maria da Silva

Qua Jun 05, 2013 11:55
Geometria Analítica
-
- [CURVAS] Equação da reta tangente e ortogonalidade
por inkz » Ter Nov 20, 2012 04:22
- 4 Respostas
- 3700 Exibições
- Última mensagem por inkz

Ter Nov 20, 2012 12:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
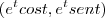
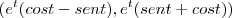



 ,
,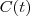 é
é 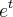 . Calcule
. Calcule 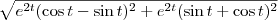
 ,
, 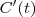 e o produto escalar
e o produto escalar 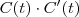 respectivamente, e substitua na equação.
respectivamente, e substitua na equação.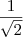 .
.


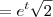 ,
,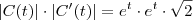 .
.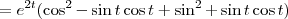
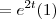 .
.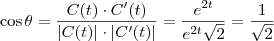 .
.


 .
.



