-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480191 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 539322 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 503197 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 726892 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2162975 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por TheKyabu » Sáb Out 27, 2012 23:24
por TheKyabu » Sáb Out 27, 2012 23:24
Bom o exercicio deve ser simples mas n to conseguindo fazer,
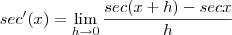
ai tentei fazer x + h = u,trocando as incognitas,mas n consegui resolver,me ajudem ai por favor

vlw
-
TheKyabu
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Out 19, 2012 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por MarceloFantini » Dom Out 28, 2012 00:32
por MarceloFantini » Dom Out 28, 2012 00:32
Não é tão simples assim, você precisa primeiro descobrir qual é a relação para secante da soma de arcos. Sabemos que
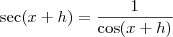
,
daí
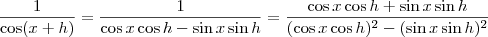
.
Parece ser uma expressão bem complicada, e desnecessária. Você não tem acesso ainda às regras de derivação usuais?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por TheKyabu » Dom Out 28, 2012 11:44
por TheKyabu » Dom Out 28, 2012 11:44
Pois é,ainda n tenho to acompanhando o livro do guidorizzi,ai to no inicio de derivadas e apareceu eses exercicio ai,
pelo q vc diz,parece q da pra resolver esses exercicio mais facilmente,com outras tecnicas de derivaçao neh
vlw ai pela ajuda
-
TheKyabu
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Out 19, 2012 19:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada pela Definiçao
por PeIdInHu » Sáb Mai 22, 2010 17:24
- 1 Respostas
- 1916 Exibições
- Última mensagem por admin

Sáb Mai 22, 2010 18:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definiçao
por tumiattibrz » Sex Mai 27, 2011 17:17
- 3 Respostas
- 2143 Exibições
- Última mensagem por LuizAquino

Sáb Mai 28, 2011 12:28
Cálculo: Limites, Derivadas e Integrais
-
- derivada pela definiçao
por paula luna » Sex Jun 10, 2011 04:41
- 2 Respostas
- 1984 Exibições
- Última mensagem por Fabio Cabral

Sex Jun 10, 2011 11:23
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela definição
por core » Qua Out 16, 2013 02:15
- 1 Respostas
- 1486 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 21:26
Cálculo: Limites, Derivadas e Integrais
-
- derivada pela definição
 por JoaoLuiz07 » Ter Fev 02, 2016 10:02
por JoaoLuiz07 » Ter Fev 02, 2016 10:02
- 1 Respostas
- 1410 Exibições
- Última mensagem por adauto martins

Qui Fev 04, 2016 15:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 44 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
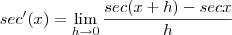


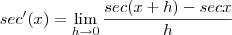


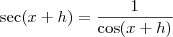 ,
,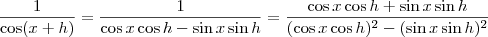 .
.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.