 por pseytow » Qua Jul 02, 2008 13:11
por pseytow » Qua Jul 02, 2008 13:11
não entendo porque o gráfico dessa expressão passa pelo ponto y=1!
ela não possui assíndota horizontal?
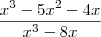
quando x tende ao infinito, tudo bem, ele não chega em y=1, mas entre raiz de oito positivo e raiz de oito negotivo existe um gráfico que não consigo entender.
-
pseytow
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jul 02, 2008 12:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Econômicas
- Andamento: cursando
 por Molina » Qui Jul 03, 2008 12:10
por Molina » Qui Jul 03, 2008 12:10
desculpe a ignorância, mas poderia explicar melhor qual a sua dúvida?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por admin » Sex Jul 04, 2008 05:39
por admin » Sex Jul 04, 2008 05:39
Olá
pseytow, boas-vindas!
O gráfico desta função é mais complicado porque podemos considerá-la como sendo um produto entre uma cúbica e uma hipérbole.
Para ressaltarmos este produto, podemos escrevê-la assim, por exemplo:
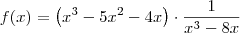
Ela possui assíntota horizontal sim, é a reta

mesmo, mas esta é somente para a "parte" hipérbólica resultante.
As outras assíntotas verticais,

e
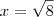
, são para a "parte" cúbica resultante.
O "Cálculo" trabalha o estudo de funções para esboços, mas nunca conseguiremos representar exatamente o gráfico de "qualquer" função. Para isso, temos a ferramenta da computação. Veja a representação desta função para você entendê-la melhor:
Agora, acrescentei as assíntotas em azul:
Espero ter ajudado e bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- assíntotas
por aquis » Qua Set 10, 2014 11:49
- 0 Respostas
- 1645 Exibições
- Última mensagem por aquis

Qua Set 10, 2014 11:49
Cálculo: Limites, Derivadas e Integrais
-
- Limites(assíntotas)
por Luciano Dias » Dom Jan 03, 2010 12:37
- 3 Respostas
- 7587 Exibições
- Última mensagem por Molina

Dom Jan 03, 2010 23:22
Cálculo: Limites, Derivadas e Integrais
-
- Assíntotas da hipérbole
por CarolMarques » Sáb Mai 26, 2012 11:41
- 1 Respostas
- 1703 Exibições
- Última mensagem por LuizAquino

Seg Mai 28, 2012 15:12
Geometria Analítica
-
- Limite - assintotas
por emsbp » Seg Jul 16, 2012 17:56
- 9 Respostas
- 5191 Exibições
- Última mensagem por skin

Ter Jul 17, 2012 15:44
Cálculo: Limites, Derivadas e Integrais
-
- Limite - Assintotas
por Viviani » Qui Jan 10, 2013 13:19
- 2 Respostas
- 1841 Exibições
- Última mensagem por Viviani

Ter Jan 15, 2013 16:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
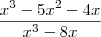

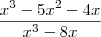


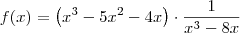
 mesmo, mas esta é somente para a "parte" hipérbólica resultante.
mesmo, mas esta é somente para a "parte" hipérbólica resultante. e
e 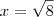 , são para a "parte" cúbica resultante.
, são para a "parte" cúbica resultante.