Estou com uma dúvida que chega a ser básica, talvez algo relacionado à fatoração.
Já tentei de todas as formas possíveis que vi (bem rápido) em certos exemplos, resolver uma integral do tipo
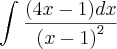
O meu problema é com o denominador, não estou chegando a resposta correta que é
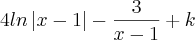
Até consigo achar o
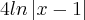
Enfim, se alguém se disponibilizar a me ajudar, agradeço desde já.


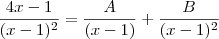
 , temos:
, temos: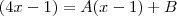
 :
: 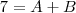
 :
: 
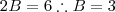 e
e  .
.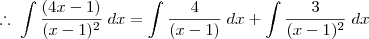
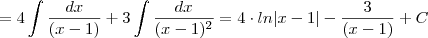



 .
.
 :
: