Queria saber como faço para identificar uma função continua, vou pegar um exemplo:
f(x) = { x + 4, se x < 2
x - 1, se x >= 2}
Aproveitando o embalo, como faço para achar o calor de L e M para que a função seja continua
f(x) = { x³ - 2x² - 5x + 6 / x² - x - 6, se x é diferente de -2 e 3
L , se x = -2
M, se x = 3}
PS: Não consegui escrever a fórmula pelo Latex


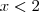 , então
, então 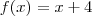 e a função é uma reta, portanto contínua.
e a função é uma reta, portanto contínua. , então
, então  e a função é uma reta, portanto contínua.
e a função é uma reta, portanto contínua. e depois de
e depois de  quando
quando  tende a
tende a  pela direita é diferente do limite quando
pela direita é diferente do limite quando 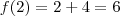 usando a lei para valores menores que
usando a lei para valores menores que 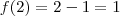 usando a lei para valores maiores que
usando a lei para valores maiores que 
