 por barizom » Ter Abr 13, 2010 22:35
por barizom » Ter Abr 13, 2010 22:35
Peguei um exercicio na interner sobre limites, como eu não indefinição dele fui olhar a resolução dele, mas fiquei confuso quanto a parte de fatoração, não sei como o cara fez para fatorar o denominador.
Formula do limite:
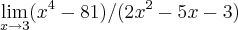
No site o denominador e no numerador depois serem fatorados ficaram assim:
![\lim_{x\rightarrow3}\left[ ({x}^{2}-9)({x}^{2}+9)} \right]/\left[ (x-3)(2x+1) \right]
{} \lim_{x\rightarrow3}\left[ ({x}^{2}-9)({x}^{2}+9)} \right]/\left[ (x-3)(2x+1) \right]
{}](/latexrender/pictures/160676dc654b65037dc574fd134b8cfe.png)
Minha duvida é como eu faço para
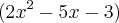
virar
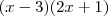
-
barizom
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Mar 27, 2010 13:39
- Formação Escolar: SUPLETIVO
- Área/Curso: Fisica
- Andamento: cursando
 por MarceloFantini » Qua Abr 14, 2010 00:55
por MarceloFantini » Qua Abr 14, 2010 00:55
Encontre uma raíz e depois divida o polinomio por

, onde

é a raíz encontrada.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Qua Abr 14, 2010 13:25
por Elcioschin » Qua Abr 14, 2010 13:25
2x² - 5x - 3 = 0 ----> Equação do 2] grau ----> Raízes x = 3 e x = - 1/2
+2x² - 5x - 3 |x - 3
-2x² + 6x.....|2x + 1
____________
........ x - 3
...... - x + 3
____________
........... 0
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por barizom » Qua Abr 14, 2010 14:51
por barizom » Qua Abr 14, 2010 14:51
No caso eu teria que dividir o polinomio pelas duas raizes?
Eu notei uma coisa se eu pegar x menos as duas raizes (2x+1) e (x-3) e multiplicar eu chego a equação do começo, isso e uma regra ou foi so coincidência mesmo?
-
barizom
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Mar 27, 2010 13:39
- Formação Escolar: SUPLETIVO
- Área/Curso: Fisica
- Andamento: cursando
 por Elcioschin » Qua Abr 14, 2010 19:59
por Elcioschin » Qua Abr 14, 2010 19:59
Não, basta dividir por uma das raízes (foi dividido pela raiz 3 por ser mais fácil).
Não é coincidência não. Sempre acontece isto. Veja porque na divisão de 36 por 3 (resto zero):
36 |3
1 .|12
.6
.6
.0
Sempre que o resto é nulo, o produto do quociente 12 pelo divisor 3 é igual ao divisor 36
Do mesmo modo (2x + 1)*(x - 3) = 2x² - 5x - 3 ---> desde que x = 3 e x = - 1/2 sejam raízes
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por barizom » Qui Abr 15, 2010 20:04
por barizom » Qui Abr 15, 2010 20:04
Obrigado pelas respostas, realmente eu não tinha tido a sacada de tirar as raízes da equação, dividir eu achei um pouco complicado, mas agora que eu sei que e so pegar o x menos as raízes ficou mais fácil fatorar.
-
barizom
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Mar 27, 2010 13:39
- Formação Escolar: SUPLETIVO
- Área/Curso: Fisica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolvendo a desigualdade...
 por Aliocha Karamazov » Qua Abr 06, 2011 19:55
por Aliocha Karamazov » Qua Abr 06, 2011 19:55
- 3 Respostas
- 2589 Exibições
- Última mensagem por Aliocha Karamazov

Qua Abr 06, 2011 23:20
Funções
-
- Resolvendo Equação Fracionária com MMC
por rapharocket » Qui Mar 03, 2011 16:28
- 0 Respostas
- 2531 Exibições
- Última mensagem por rapharocket

Qui Mar 03, 2011 16:28
Sistemas de Equações
-
- Resolvendo como sistema
por sullivan » Sex Dez 23, 2011 15:27
- 4 Respostas
- 2085 Exibições
- Última mensagem por sullivan

Qua Dez 28, 2011 08:57
Matemática Financeira
-
- Resolvendo equacção do terceiro grau
por jptuga » Sáb Set 17, 2011 06:02
- 2 Respostas
- 1656 Exibições
- Última mensagem por jptuga

Dom Set 18, 2011 08:58
Polinômios
-
- [calculo] Resolvendo esse problema
por amanda s » Sáb Nov 16, 2013 17:21
- 1 Respostas
- 2005 Exibições
- Última mensagem por Pessoa Estranha

Sáb Nov 16, 2013 21:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
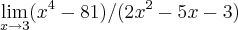
![\lim_{x\rightarrow3}\left[ ({x}^{2}-9)({x}^{2}+9)} \right]/\left[ (x-3)(2x+1) \right]
{} \lim_{x\rightarrow3}\left[ ({x}^{2}-9)({x}^{2}+9)} \right]/\left[ (x-3)(2x+1) \right]
{}](/latexrender/pictures/160676dc654b65037dc574fd134b8cfe.png)
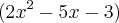 virar
virar 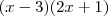

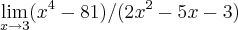
![\lim_{x\rightarrow3}\left[ ({x}^{2}-9)({x}^{2}+9)} \right]/\left[ (x-3)(2x+1) \right]
{} \lim_{x\rightarrow3}\left[ ({x}^{2}-9)({x}^{2}+9)} \right]/\left[ (x-3)(2x+1) \right]
{}](/latexrender/pictures/160676dc654b65037dc574fd134b8cfe.png)
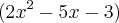 virar
virar 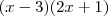

 , onde
, onde  é a raíz encontrada.
é a raíz encontrada.





![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)