



![y={x}^{2}+(a/x)...y'=({x}^{2})'+a.(1/x)'
y=2x+(-1).a/({x}^{2})\Rightarrow y'=0
(2.{x}^{3}-a)/({x}^{2})=0\Rightarrow x\neq 0...{x}^{3}=a/2
x=\sqrt[3]{a/2} y={x}^{2}+(a/x)...y'=({x}^{2})'+a.(1/x)'
y=2x+(-1).a/({x}^{2})\Rightarrow y'=0
(2.{x}^{3}-a)/({x}^{2})=0\Rightarrow x\neq 0...{x}^{3}=a/2
x=\sqrt[3]{a/2}](/latexrender/pictures/4c822729645a84e05051dc74c274a453.png)
![x=\sqrt[3]{a/2} x=\sqrt[3]{a/2}](/latexrender/pictures/59de4b441ea97f7b6a8e7d0387e25e34.png) é ponto de maximo ou minimo,devemos calcular a derivada segunda nesse ponto,entao:
é ponto de maximo ou minimo,devemos calcular a derivada segunda nesse ponto,entao: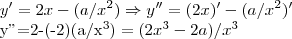
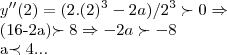
![y''(\sqrt[3]{a/2})\prec 0...
y''(\sqrt[3]{a/2})=(2.{\sqrt[3]{a/2}}^{3}-2a)/({\sqrt[3]{a/2}}^{3})
(2.(a/2)-2a)/(a/2)\prec 0\Rightarrow
a-2a\prec (a/2)\Rightarrow -1\prec (1/2) y''(\sqrt[3]{a/2})\prec 0...
y''(\sqrt[3]{a/2})=(2.{\sqrt[3]{a/2}}^{3}-2a)/({\sqrt[3]{a/2}}^{3})
(2.(a/2)-2a)/(a/2)\prec 0\Rightarrow
a-2a\prec (a/2)\Rightarrow -1\prec (1/2)](/latexrender/pictures/2bac1080c6f0eac26a38b740bf12bebd.png)
![y''(\sqrt[3]{a/2})=(2.{\sqrt[3]{a/2}}^{3}-2a)/({\sqrt[3]{a/2}}^{3})
y''(\sqrt[3]{a/2})=(2(a/2)-2a)/(a/2)=2(a-2a)/a=-2\prec 0... y''(\sqrt[3]{a/2})=(2.{\sqrt[3]{a/2}}^{3}-2a)/({\sqrt[3]{a/2}}^{3})
y''(\sqrt[3]{a/2})=(2(a/2)-2a)/(a/2)=2(a-2a)/a=-2\prec 0...](/latexrender/pictures/29fef2115f60e270b9e5d22da0f3d4a1.png)
![x=\sqrt[3]{a/2} x=\sqrt[3]{a/2}](/latexrender/pictures/59de4b441ea97f7b6a8e7d0387e25e34.png)


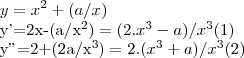
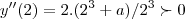
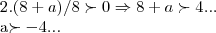
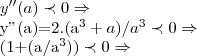
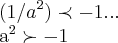
![\Rightarrow a\succ \sqrt[]{-1} \Rightarrow a\succ \sqrt[]{-1}](/latexrender/pictures/4b67b09322cf834cb2409d4835cce297.png)


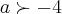 ,que eu cheguei e vc no que acabaste de concluir...anterormente,cheguei que y tera maximo ou minimo em
,que eu cheguei e vc no que acabaste de concluir...anterormente,cheguei que y tera maximo ou minimo em ![x=\sqrt[3]{a/2} x=\sqrt[3]{a/2}](/latexrender/pictures/59de4b441ea97f7b6a8e7d0387e25e34.png) ...logo,para x=2,teriamos
...logo,para x=2,teriamos![\sqrt[3]{a/2}=2\Rightarrow (a/2)=8...a=16... \sqrt[3]{a/2}=2\Rightarrow (a/2)=8...a=16...](/latexrender/pictures/4f5344b66be4819e6b2cdd2bb0c49bfa.png) foi o que vc fez,e esta correto...e que f''(2) é positivo,logo ter minimo...nessas condiçoes esta correto...
foi o que vc fez,e esta correto...e que f''(2) é positivo,logo ter minimo...nessas condiçoes esta correto...
![y''(\sqrt[3]{(a/2)})=2+(2a/{\sqrt[3]{(a/2)}}^{3})=2+(2a/(a/2))
y''(\sqrt[3]{(a/2)})=2+4=6\succ 0... y''(\sqrt[3]{(a/2)})=2+(2a/{\sqrt[3]{(a/2)}}^{3})=2+(2a/(a/2))
y''(\sqrt[3]{(a/2)})=2+4=6\succ 0...](/latexrender/pictures/1523a8b3e751d2cdb5af7b2b985311ce.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)