 por hugohggomes » Sáb Jun 25, 2016 18:38
por hugohggomes » Sáb Jun 25, 2016 18:38
Boa Tarde!
Gostaria da ajuda de alguém para demonstrar que os valores dos seguintes limites são:
a)
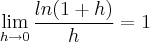
b)
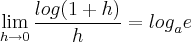
Agradeço desde já!

-
hugohggomes
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jun 09, 2016 20:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por vitor_jo » Dom Jul 10, 2016 05:36
por vitor_jo » Dom Jul 10, 2016 05:36
Na primeira, ela satisfaz as condições para o uso de L'Hopital, então basta derivar em cima e embaixo, jogar o limite e pronto.
Na segunda, note
1/h*log(1+h) = log(1+h)^1/h
Pela propriedade de limite, log(lim(1+h)^1/h)
Chamando h=1/t, t=1/h, se h->o, t->00
Assim,
log(lim(1+1/t)^t)=log e, do fato em que lim x >00 (1+1/x)^x=e
(a resposta é dada log ae pois pode ser log em qualquer base aí (só 'log' e alude a ser log na base 10...enfim).
Abraço
OBS/EDITADO... pensando bem, esse log ae pode ser algo que deixei passar. Ja não estou mais tão certo da resposta.
-
vitor_jo
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qua Jan 14, 2015 05:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas de equações exponencias (ajudem pfvr urgente)
por wtfmylena » Dom Dez 08, 2013 21:37
- 1 Respostas
- 3879 Exibições
- Última mensagem por e8group

Seg Dez 09, 2013 14:26
Equações
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5408 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4753 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4779 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4807 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


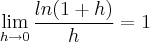
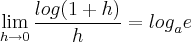





 , avisa que eu resolvo.
, avisa que eu resolvo.

