 por marinalcd » Ter Jun 14, 2016 20:21
por marinalcd » Ter Jun 14, 2016 20:21
Alguém pode me ajudar a montar a equação para resolver. Não estou conseguindo.
A prefeitura de determinada localidade decidiu mudar a taxa de fluorização da água que os habitantes usam. No reservatório local, que possui 300 mil metros cúbicos de água, há 2000 kg de flúor. O consumo médio de água na cidade é de 3 mil metros cúbicos por dia e a água utilizada é reposta com fluorização de 100 gramas de fluor por m3. Determine a quantidade de flúor no reservatório em um tempo t qualquer.
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por adauto martins » Qua Jun 22, 2016 12:31
por adauto martins » Qua Jun 22, 2016 12:31
seja
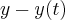
a quantidade de liquido(ou fluido) em um reservatorio em um dado instante,temos q.:
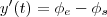
,onde
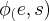
é o fluxo de entrada/saida,entao,desenvolvendo a EDO, teremos:
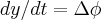
,onde
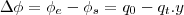
,variaçao do fluxo de entrada/saida,onde q(t) quantidade de liquido(fluido)...
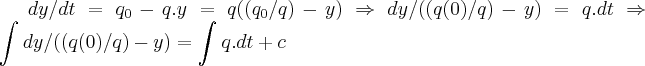
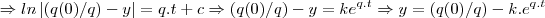
...p/t=0
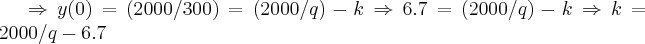
,entao:
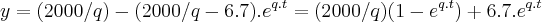
...p/t=24h
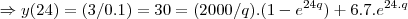
,bom agora é achar q. calcule restante...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação diferencial] Problema de valor inicial
por Aliocha Karamazov » Qua Fev 15, 2012 23:34
- 2 Respostas
- 1800 Exibições
- Última mensagem por Aliocha Karamazov

Qui Fev 23, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12211 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
-
- Equaçao diferencial
por romulo39 » Dom Abr 03, 2011 20:58
- 1 Respostas
- 3941 Exibições
- Última mensagem por LuizAquino

Seg Abr 04, 2011 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial
por jacquelline » Qui Mai 17, 2012 11:04
- 2 Respostas
- 2073 Exibições
- Última mensagem por jacquelline

Sáb Mai 19, 2012 20:37
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 1
por Cleyson007 » Qua Nov 07, 2012 21:09
- 8 Respostas
- 3852 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 17:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


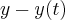 a quantidade de liquido(ou fluido) em um reservatorio em um dado instante,temos q.:
a quantidade de liquido(ou fluido) em um reservatorio em um dado instante,temos q.: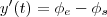 ,onde
,onde 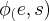 é o fluxo de entrada/saida,entao,desenvolvendo a EDO, teremos:
é o fluxo de entrada/saida,entao,desenvolvendo a EDO, teremos: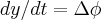 ,onde
,onde 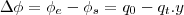 ,variaçao do fluxo de entrada/saida,onde q(t) quantidade de liquido(fluido)...
,variaçao do fluxo de entrada/saida,onde q(t) quantidade de liquido(fluido)...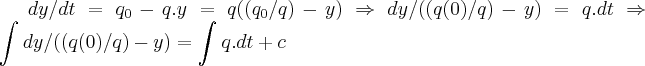
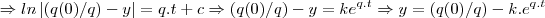 ...p/t=0
...p/t=0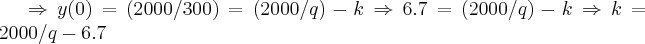 ,entao:
,entao: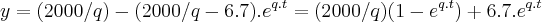 ...p/t=24h
...p/t=24h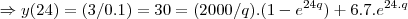 ,bom agora é achar q. calcule restante...
,bom agora é achar q. calcule restante... em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.