Começamos com um resultado :
Seja
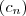
uma sequencia de termos positivos . Suponhamos que exista uma sequencia
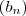
convergente para zero (i.e, (*)
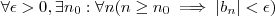
) (Notação :
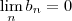
ou
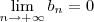
) tal que a parti de um certo índice
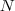
, todos termos
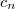
, com
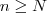
não excede a
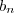
, i.e,
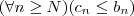
, então a sequencia
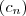
tbm converge para zero .
Dicas p prova : Use a hipótese de
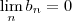
. Use a definição (*) . Depois tome M como o máximo entre n_0 e N . Observe que para todo n maior igual a M vc terá valida (*) e tbm a segunda desigualdade que majora os c_n's , com n > N .
.
Seu exercício segue como um corolário do resultado acima : Defina
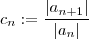
. Por hipótese
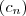
converge para
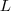
. Suponhamos que
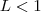
. Nota que
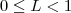
Fixemos um número que

. Como (c_n) converge para L , podemos encontrar
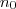
tal que
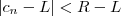
vale sempre que
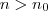
.
Logo , para todo

. Donde , para todo
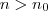
,
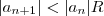
. Em virtude desta desigualdade (recursiva ) nota o seguinte :
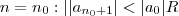

(...)
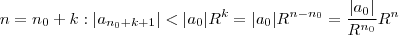
.
Não é dificil provar por indução que vale

.
Chame
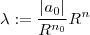
e ponha
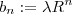
.
Exercício : Mostre que
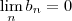
e conclua que
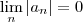
.
Obs.:
"
Em primeiro lugar, não consigo interpretar o que seria o índice n do {a}_{n} tendendo a infinito. Significa algum valor muito grande? Posso considerar o {a}_{n} como sendo "infinito" (e nesse caso o resultado L do limite seria 1)? A seguir, o que significa mostrar que o limite é menor que 1? Como mostrar que ele tende a zero? "
Uma sequência num conjunto

é meramente uma função
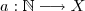
, em que denotamos a imagem de

por

por
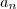
ao invés da notação tradicional
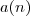
. Para denotar esta função especial simplesmente escrevemos
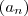
ou

ou simplesmente
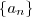
. Note que

é só um conjunto .Exemplos :
i) Consideremos um circulo unitário S contido no
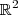
. Dado um número natural

. Denote o (único ) polígono regular
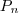
inscrito no circulo S . ( Por exemplo , P_3 é um triangulo equilátero , P_4 Quadrado , .... ) . Seja X o conjunto de todos estes polígonos P_n . Nota que a correspondência ,
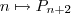
define uma aplicação
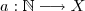
, i.e.,
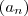
é uma sequencia cujo o n-esimo termo é dado por
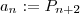
. Observe que a medida que n cresce , o polígono fica cada vez mais 'parecido' com o circulo S ... Este comportamento nos leva a conjectura que esta sequencia converge para o circulo

em notação isto seria dizer
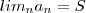
. Mas infelizmente , a priori , não podemos responder esta questão . Para tal deveríamos introduzir em X , uma topologia , onde X munido desta topologia seria o que chamamos de
espaço topológico , onde poderíamos responder com precisão se tal sequencia convergiria ou não para o Circulo .
ii) Seja
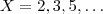
o conjunto de todos os primos em
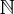
então existe uma (única ) bijeção crescente
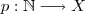
, i.e ,
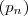
é uma sequencia em

crescente
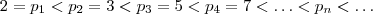
. Pela infinitude dos números primos esta sequência não pode ser limitada , logo em particular tal sequencia não é convergente ,
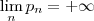
.
iii) Seja
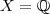
. Observe que para cada
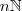
,
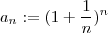
é uma número racional . Esta correspondência define uma sequencia
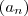
em

a qual nao converge em

. Mas , converge em

.
iV) Seja
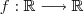
uma função tal que
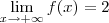
.(limite usual calculo 1) . Note que esta função restrita a
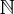
é uma sequência
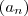
em

dada por
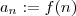
.
É possível mostrar sem dificuldade que esta sequência tbm converge para 2 .
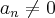 para todo
para todo 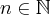 e que o limite
e que o limite  existe. Mostre que se
existe. Mostre que se  , então
, então 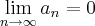 .
. tendendo a infinito. Significa algum valor muito grande? Posso considerar o
tendendo a infinito. Significa algum valor muito grande? Posso considerar o  como sendo "infinito" (e nesse caso o resultado L do limite seria 1)? A seguir, o que significa mostrar que o limite é menor que 1? Como mostrar que ele tende a zero?
como sendo "infinito" (e nesse caso o resultado L do limite seria 1)? A seguir, o que significa mostrar que o limite é menor que 1? Como mostrar que ele tende a zero?

 seria um dos exemplos dessa situação. Porém, uma vez que a questão pede uma demonstração rigorosa e geral, estou com dificuldade de organizar uma linha de raciocínio.
seria um dos exemplos dessa situação. Porém, uma vez que a questão pede uma demonstração rigorosa e geral, estou com dificuldade de organizar uma linha de raciocínio.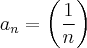
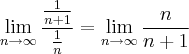 que converge inferiormente para 1.
que converge inferiormente para 1.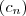 uma sequencia de termos positivos . Suponhamos que exista uma sequencia
uma sequencia de termos positivos . Suponhamos que exista uma sequencia 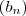 convergente para zero (i.e, (*)
convergente para zero (i.e, (*) 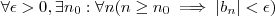 ) (Notação :
) (Notação : 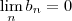 ou
ou 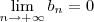 ) tal que a parti de um certo índice
) tal que a parti de um certo índice 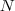 , todos termos
, todos termos 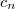 , com
, com 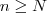 não excede a
não excede a 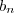 , i.e,
, i.e, 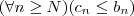 , então a sequencia
, então a sequencia 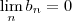 . Use a definição (*) . Depois tome M como o máximo entre n_0 e N . Observe que para todo n maior igual a M vc terá valida (*) e tbm a segunda desigualdade que majora os c_n's , com n > N .
. Use a definição (*) . Depois tome M como o máximo entre n_0 e N . Observe que para todo n maior igual a M vc terá valida (*) e tbm a segunda desigualdade que majora os c_n's , com n > N . 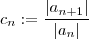 . Por hipótese
. Por hipótese 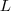 . Suponhamos que
. Suponhamos que 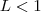 . Nota que
. Nota que 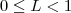 Fixemos um número que
Fixemos um número que  . Como (c_n) converge para L , podemos encontrar
. Como (c_n) converge para L , podemos encontrar 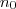 tal que
tal que 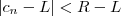 vale sempre que
vale sempre que 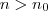 .
.  . Donde , para todo
. Donde , para todo 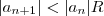 . Em virtude desta desigualdade (recursiva ) nota o seguinte :
. Em virtude desta desigualdade (recursiva ) nota o seguinte : 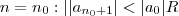

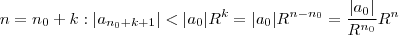 .
.  .
.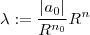 e ponha
e ponha 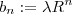 .
. 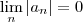 .
.  é meramente uma função
é meramente uma função 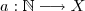 , em que denotamos a imagem de
, em que denotamos a imagem de  por
por  por
por 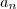 ao invés da notação tradicional
ao invés da notação tradicional 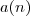 . Para denotar esta função especial simplesmente escrevemos
. Para denotar esta função especial simplesmente escrevemos 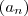 ou
ou  ou simplesmente
ou simplesmente 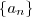 . Note que
. Note que 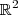 . Dado um número natural
. Dado um número natural  . Denote o (único ) polígono regular
. Denote o (único ) polígono regular 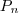 inscrito no circulo S . ( Por exemplo , P_3 é um triangulo equilátero , P_4 Quadrado , .... ) . Seja X o conjunto de todos estes polígonos P_n . Nota que a correspondência ,
inscrito no circulo S . ( Por exemplo , P_3 é um triangulo equilátero , P_4 Quadrado , .... ) . Seja X o conjunto de todos estes polígonos P_n . Nota que a correspondência , 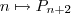 define uma aplicação
define uma aplicação 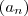 é uma sequencia cujo o n-esimo termo é dado por
é uma sequencia cujo o n-esimo termo é dado por 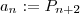 . Observe que a medida que n cresce , o polígono fica cada vez mais 'parecido' com o circulo S ... Este comportamento nos leva a conjectura que esta sequencia converge para o circulo
. Observe que a medida que n cresce , o polígono fica cada vez mais 'parecido' com o circulo S ... Este comportamento nos leva a conjectura que esta sequencia converge para o circulo  em notação isto seria dizer
em notação isto seria dizer 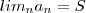 . Mas infelizmente , a priori , não podemos responder esta questão . Para tal deveríamos introduzir em X , uma topologia , onde X munido desta topologia seria o que chamamos de
. Mas infelizmente , a priori , não podemos responder esta questão . Para tal deveríamos introduzir em X , uma topologia , onde X munido desta topologia seria o que chamamos de 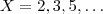 o conjunto de todos os primos em
o conjunto de todos os primos em 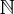 então existe uma (única ) bijeção crescente
então existe uma (única ) bijeção crescente 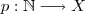 , i.e ,
, i.e , 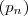 é uma sequencia em
é uma sequencia em 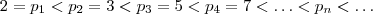 . Pela infinitude dos números primos esta sequência não pode ser limitada , logo em particular tal sequencia não é convergente ,
. Pela infinitude dos números primos esta sequência não pode ser limitada , logo em particular tal sequencia não é convergente , 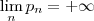 .
. 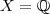 . Observe que para cada
. Observe que para cada 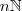 ,
, 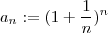 é uma número racional . Esta correspondência define uma sequencia
é uma número racional . Esta correspondência define uma sequencia  .
.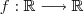 uma função tal que
uma função tal que 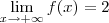 .(limite usual calculo 1) . Note que esta função restrita a
.(limite usual calculo 1) . Note que esta função restrita a 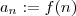 .
. 
 .
. ,
,  e para
e para  ,
,  .
.
 , monte a função e substitua
, monte a função e substitua  por
por  .
.
