 por catabluma123 » Qua Fev 10, 2016 21:06
por catabluma123 » Qua Fev 10, 2016 21:06
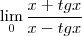
fiz da seguinte forma:
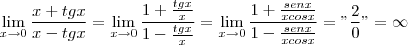
o resultado na realidade é

, mas não entendo como fazer a analise do sinal do

. alguém poderia me ajudar?
-
catabluma123
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Fev 10, 2016 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia mecânica
- Andamento: cursando
 por adauto martins » Seg Fev 15, 2016 15:14
por adauto martins » Seg Fev 15, 2016 15:14
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Cleyson007 » Seg Fev 15, 2016 16:02
por Cleyson007 » Seg Fev 15, 2016 16:02
Fazendo
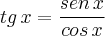
, temos:
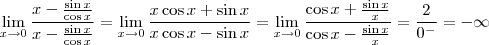
Observe também que utilizei o limite fundamental
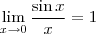
.
O resultado é negativo pois, para valores próximos à zero (ou seja, à esquerda ou à direita) o cosseno é negativo).
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Seg Fev 15, 2016 16:12
por Cleyson007 » Seg Fev 15, 2016 16:12
Fazendo
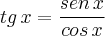
, temos:
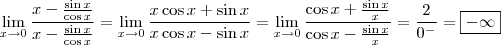
Observe também que utilizei o limite fundamental
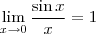
.
O resultado é negativo pois, para valores próximos à zero (ou seja, à esquerda ou à direita) o cosseno é negativo).
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por adauto martins » Seg Fev 15, 2016 18:57
por adauto martins » Seg Fev 15, 2016 18:57
caro colega cleydson...
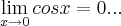
,logo em sua resoluçao ficaria...
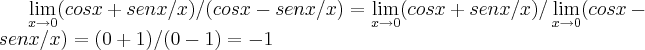
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Fev 15, 2016 19:17
por adauto martins » Seg Fev 15, 2016 19:17
desculpe ai colega cleyson...comi um erro fundamental...
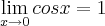
mas reveja minha soluçao,q. é o valor de tal limite...esse limite é -1,e nao

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Ter Fev 16, 2016 14:59
por adauto martins » Ter Fev 16, 2016 14:59
é vc esta com a razao caro prof.cleyson...comi um erro,q. verifiquei com expansao de series de taylor da funçao tg...no mais obrigado,adauto martins
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Cleyson007 » Ter Fev 16, 2016 19:10
por Cleyson007 » Ter Fev 16, 2016 19:10
Sem problemas amigo..
Abraço,
Prof° Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por adauto martins » Qua Fev 17, 2016 11:27
por adauto martins » Qua Fev 17, 2016 11:27
resolvendo a questao do fator negativo,duvida do colega catabluma...
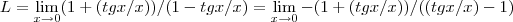
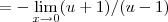
... onde u=tgx/x
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cáculo de uma derivada
por jmario » Qua Abr 28, 2010 13:41
- 20 Respostas
- 16160 Exibições
- Última mensagem por jmario

Sex Mai 07, 2010 13:56
Cálculo: Limites, Derivadas e Integrais
-
- Exercícios - Cáculo III
 por HenriqueGS » Dom Jun 05, 2016 20:37
por HenriqueGS » Dom Jun 05, 2016 20:37
- 1 Respostas
- 1196 Exibições
- Última mensagem por adauto martins

Ter Jun 07, 2016 12:18
Cálculo: Limites, Derivadas e Integrais
-
- Cáculo - Limites - função contínua num intervalo
por Antonio H V Araujo » Sáb Nov 14, 2015 22:24
- 1 Respostas
- 2578 Exibições
- Última mensagem por Cleyson007

Seg Nov 16, 2015 07:29
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6646 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
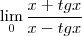
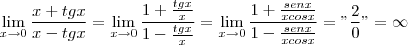
 , mas não entendo como fazer a analise do sinal do
, mas não entendo como fazer a analise do sinal do . alguém poderia me ajudar?
. alguém poderia me ajudar?
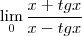
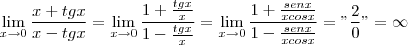
 , mas não entendo como fazer a analise do sinal do
, mas não entendo como fazer a analise do sinal do . alguém poderia me ajudar?
. alguém poderia me ajudar?

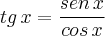 , temos:
, temos: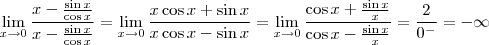
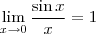 .
.
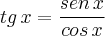 , temos:
, temos: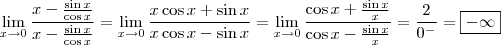
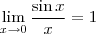 .
.
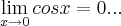 ,logo em sua resoluçao ficaria...
,logo em sua resoluçao ficaria...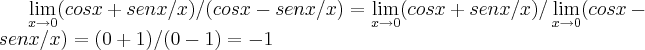

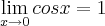





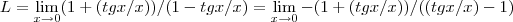
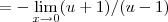 ... onde u=tgx/x
... onde u=tgx/x