Primeiramente esta função não possui limite. Nem "+infinito" nem "-infinito", esta função simplesmente não possui uma tendencia quando se aproxima de 0 (zero).
Lembra que pra que o limite exista, o limite pela esquerda e pela direita (0- e 0+) tem de ser iguais, o que não ocorre para esta função. Quando fazemos o limite pela esquerda e pela direita temos duas respostas diferentes, como segue:
Pela esquerda (0-)
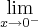


Pela direita (0+)
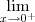


Como tu podes ver os limites são diferentes e, portanto, o limite de 1/x quando este se aproxima de 0 não existe. Vale lembrar que alguns autores consideram que limites com resposta infinita ( tanto +inf quanto -inf) como uma não existencia do limite, logo é bom cuidar este tipo de informação que pode confundir bastante.
Ja quanto a tua pergunta de por que o limite cresce a medida que se aproxima de um valor (limite "explode") é bem simples. Isto normalmente acontece quando a variavel do limite esta tendendo para um "zero" do denominador da função (um polo). Em 1/x , por exemplo, o denominador tem como "zero" (raiz) o numero 0.
Agora imagina que estamos nos aproximando de 0, quanto mais nos aproximamos, menor o valor é, por exemplo, x->1 , x->0.1 , x->0.01 , ... , x->0.0000000001 e quando computamos estes valores na função, o valor dela começa a aumentar indefinidamente, ou seja, quando x->0 o valor da função é tao grande que podemos dizer que tende ao infinito.
Exemplo:
f(x) = 1/x => f(0.00000000000001) = 100.000.000.000.000
f(x) = 1/x => f(-0.00000000000000000000001) = -100.000.000.000.000.000.000.000
Um bom exemplo para avaliar isto é a função 1/(x² - 1) ,pois para esta função, sim, temos um limite infinito quando a função se aproxima de 1 (ou -1).
Observe que tanto o limite pela esquerda e pela direita são iguais valendo infinito.
Espero ter ajudado, bons estudos!
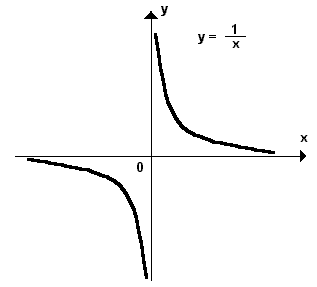


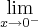




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.