Nao estou conseguindo a resolução de problema:
Uma placa circular plana tem o formato da região x^2 + y^2 ?1. A placa, incluindo a
fronteira na qual x^2 + y^2 =1 é aquecida, de forma que a temperatura no ponto (x,y)
é dada pela equação T(x, y)= x^2 + 2y^2 ? x . Encontre as temperaturas nos pontos
mais quentes e mais frios da placa?


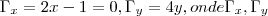 sao as derivadas parciais em relaçao a x,y
sao as derivadas parciais em relaçao a x,y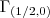 =-1/2...
=-1/2...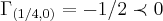 e
e 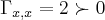 ,onde
,onde 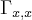 e a derivada segunda no ponto (1/2,0)...vamos procurar a direçao do gradiente,onde a funçao procura seu max...entao:
e a derivada segunda no ponto (1/2,0)...vamos procurar a direçao do gradiente,onde a funçao procura seu max...entao: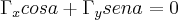

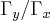
 (
(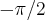 ,
,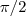 )e
)e 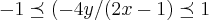 ,faz-se os calculos achando a e subst. na expressao do gradiente,tem-se o ponto de max. e o valor da temp. max...
,faz-se os calculos achando a e subst. na expressao do gradiente,tem-se o ponto de max. e o valor da temp. max...
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.